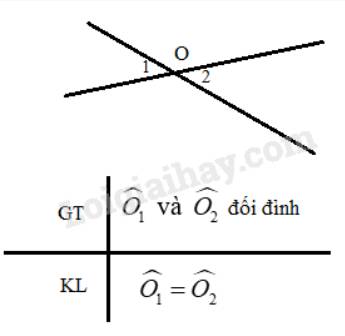
nêu giả thiết và kết luận của định lý sau : Ví Dụ "nếu 2 góc đối đỉnh thì bằng nhau"

Những câu hỏi liên quan
Bài 1,Viết giả thiết và kết luận chứng minh các định lý sau nếu hai góc có cảnh tương ứng vuông góc thì a,chúng bằng nhau nếu chúng cùng tù hoặc cùng nhọnb,chúng bù nhau nếu góc này nhọn góc kia tùBài 2,vẽ hình và Viết giả thiết kết luận và chứng minh định lý sau nếu hai góc có cạnh tương ứng song song thì:a,chúng bằng nhau nếu chúng cùng tù hoặc cùng nhọnb,chúng bù nhau nếu góc này nhọn góc tùBài 3,Viết giả thiết kết luận và chứng minh định lí sau : Hai tia phân giác của hai góc đối đỉnh thì...
Đọc tiếp
Bài 1,Viết giả thiết và kết luận chứng minh các định lý sau nếu hai góc có cảnh tương ứng vuông góc thì
a,chúng bằng nhau nếu chúng cùng tù hoặc cùng nhọn
b,chúng bù nhau nếu góc này nhọn góc kia tù
Bài 2,vẽ hình và Viết giả thiết kết luận và chứng minh định lý sau nếu hai góc có cạnh tương ứng song song thì:
a,chúng bằng nhau nếu chúng cùng tù hoặc cùng nhọn
b,chúng bù nhau nếu góc này nhọn góc tù
Bài 3,Viết giả thiết kết luận và chứng minh định lí sau : Hai tia phân giác của hai góc đối đỉnh thì đối nhau
Vẽ hình và viết giả thiết, kết luận của định lí:
“Hai góc đối đỉnh thì bằng nhau”
Bài 1: Vẽ hình và viết giả thiết, kết luận và chứng minh các định lý sau Nếu 2 góc có cạnh tương úng vuông góc thìa) Chúng bằng nhau nếu chúng cùng tù hoặc cùng nhọn.b) Chúng bù nhau nếu góc này nhọn, góc kia tù.Bài 2: Vẽ hình, viết giả thiết, kết luận của định lý sau: Nếu 2 góc có cạnh tương ứng song song thìa) Chúng bằng nhau nếu chúng cùng tù hoặc cùng nhọnb) Chúng bù nhau nếu góc này nhọn, góc kia tù.
Đọc tiếp
Bài 1: Vẽ hình và viết giả thiết, kết luận và chứng minh các định lý sau "Nếu 2 góc có cạnh tương úng vuông góc thì"
a) Chúng bằng nhau nếu chúng cùng tù hoặc cùng nhọn.
b) Chúng bù nhau nếu góc này nhọn, góc kia tù.
Bài 2: Vẽ hình, viết giả thiết, kết luận của định lý sau: "Nếu 2 góc có cạnh tương ứng song song thì"
a) Chúng bằng nhau nếu chúng cùng tù hoặc cùng nhọn
b) Chúng bù nhau nếu góc này nhọn, góc kia tù.
Bài 1:
a)Chúng cùng tù hoặc cùng nhọn( giả thiết )
Chúng bằng nhau( kết luận )
b) Góc này nhọn, góc kia tù ( giả thiết )
Chúng bù nhau ( kết luận )
Bài 2:
a)( hình trên ) Chúng cùng tù cùng nhọn( Giả thiết)
Chúng bằng nhau ( kết luận )
b) Góc này nhọn, góc kia tù ( giả thiết )
Chúng bù nhau ( kết luận )
Đúng 0
Bình luận (0)
Vẽ hình và viết giả thiết, kết luận của định lý (viết bằng ký hiệu ) "Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau".Vẽ hình và viết giả thiết, kết luận của định lý (viết bằng ký hiệu ) "Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau"
a: Giả thiết: a//b
Kết luận: \(\widehat{A_1}=\widehat{B_1}\)
Đúng 0
Bình luận (0)
Cho định lí:
“ Nếu hai góc đối đỉnh thì hai góc đó bằng nhau”.
a) Vẽ hình minh họa nội dung định lí trên.
b) Viết giả thiết và kết luận của định lí trên.
c) Chứng tỏ định lí trên là đúng.
a)
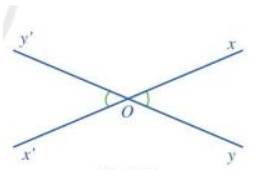
b)
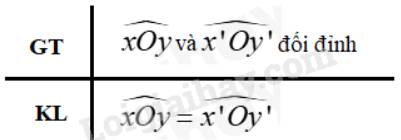
c) Vì góc xOy và x’Oy’ là hai góc đối đỉnh nên Oy và Oy’ là hai tia đối nhau; Ox và Ox’ là hai tia đối nhau
\( \Rightarrow \widehat {xOy}\) và \(\widehat {xOy'}\) là hai góc kề bù; \(\widehat {xOy'}\) và \(\widehat {x'Oy'}\) là hai góc kề bù
\( \Rightarrow \widehat {xOy} + \widehat {xOy'} = 180^\circ \); \(\widehat {xOy'} + \widehat {x'Oy'} = 180^\circ \) ( tính chất 2 góc kề bù)
\( \Rightarrow \)\(\widehat {xOy} = \widehat {x'Oy'}\) (đpcm)
Đúng 0
Bình luận (0)
Vẽ hình , ghi giả thiết và chứng minh định lý sau : " 2 góc đối đỉnh thì bằng nhau "
Chứng minh
Ta có O1 + O3 =180o (vì hai góc kề bù) (1)
O2+O3=180o (vì hai góc kề bù ) (2)
Từ (1) và (2) => O1+O2=O2+O3 =>O1=O2
Đúng 0
Bình luận (0)
Vẽ hình, ghi giả thiết, kết luận và chứng minh định lí :"Hai góc đối đỉnh thì bằng nhau"
| Giả thiết | Góc O1 và góc O3 đối đỉnh |
| Kết luận | Góc O1 = Góc O3 |
C/m :
Ta có :
\(\begin{cases}\widehat{O_1}+\widehat{O_2}=180^0\\\widehat{O_3}+\widehat{O_2}=180^0\end{cases}\) ( kề bù )
\(\Rightarrow\begin{cases}\widehat{O_1}=180^0-\widehat{O_2}\\\widehat{O_3}=180^0-\widehat{O_2}\end{cases}\)
\(\Rightarrow\widehat{O_1}=\widehat{O_3}\left(đpcm\right)\)
Đúng 1
Bình luận (2)
Bài 2 : Cho tỉ lệ thức frac{3x-y}{x+y} frac{3}{4}.Tìm giá trị của tỉ số x , yBài 3 : Vẽ hình ghi giả thiết , kết luận và chứng minh định lý sau :a/Nếu một đường thẳng cắt hai đường thẳng song song thì các tia phân giác của mỗi cặp góc đồng vị song song với nhaub/Số đo của góc tạo bởi tia phân giác với mỗi cạnh của góc bằng nửa số đo của góc ấyc/Hai góc đối đỉnh thì bằng nhauVẽ hình ghi giả thiết , kết luận và chứng minh định lý sau :Bài 4 :Nếu một đường thẳng cắt hai đường thẳng song song thìa/...
Đọc tiếp
Bài 2 : Cho tỉ lệ thức \(\frac{3x-y}{x+y}\) = \(\frac{3}{4}\).Tìm giá trị của tỉ số x , y
Bài 3 : Vẽ hình ghi giả thiết , kết luận và chứng minh định lý sau :
a/Nếu một đường thẳng cắt hai đường thẳng song song thì các tia phân giác của mỗi cặp góc đồng vị song song với nhau
b/Số đo của góc tạo bởi tia phân giác với mỗi cạnh của góc bằng nửa số đo của góc ấy
c/Hai góc đối đỉnh thì bằng nhau
Vẽ hình ghi giả thiết , kết luận và chứng minh định lý sau :
Bài 4 :Nếu một đường thẳng cắt hai đường thẳng song song thì
a/Hai góc đồng vị = nhau
b/Hai góc trong cùng phía bù nhau
c/Hai góc so le trong bằng nhau
\(\frac{3x-y}{x+y}=\frac{3}{4}\)
\(\Leftrightarrow4\left(3x-y\right)=3\left(x+y\right)\)
\(\Leftrightarrow12x-4y=3x+3y\)
\(\Leftrightarrow12x-4y-3x-3y=0\)
\(\Leftrightarrow9x-7y=0\)
\(\Leftrightarrow9x=7y\Leftrightarrow\frac{x}{7}=\frac{y}{9}\)
Đúng 1
Bình luận (0)
Vẽ hình, ghi giả thiết kết luận và chứng minh định lí hai góc đối đỉnh thì bằng nhau
Vì góc O1 và góc O2 kề bù => O1 + O2 = 180o
Góc góc O2 và góc O3 kề bù => O2 + O3 = 180o
=> O1 = O2
Đúng 0
Bình luận (0)
Xem thêm câu trả lời