Đặt \(-x^2+2x=t\Rightarrow0\le t\le1\)

\(\Rightarrow-t^2+t-3+m=0\)

\(\Leftrightarrow t^2-t+3=m\)

Xét hàm \(f\left(t\right)=t^2-t+3\) trên \(\left[0;1\right]\)

\(-\dfrac{b}{2a}=\dfrac{1}{2}\in\left[0;1\right]\)

\(f\left(0\right)=3\) ; \(f\left(1\right)=3\) ; \(f\left(\dfrac{1}{2}\right)=\dfrac{11}{4}\)

\(\Rightarrow\dfrac{11}{4}\le f\left(t\right)\le3\)

\(\Rightarrow\) Pt có nghiệm khi và chỉ khi \(\dfrac{11}{4}\le m\le3\)

Đáp án C

Phương pháp:

phương trình trở thành

=> Hàm số đồng biến trên khoảng [2;+∞)

Để phương trình (*) có nghiệm thì 2m ≥ 6 ⇔ m ≥ 3

Đáp án B

\(x-4\sqrt{x+3}+m=0\)

\(\Leftrightarrow x+3-4\sqrt{x+3}-3+m=0\left(1\right)\)

\(đăt:\sqrt{x+3}=t\left(t\ge0\right)\)

\(\left(1\right)\Leftrightarrow t^2-4t-3+m=0\Leftrightarrow f\left(t\right)=t^2-4t-3=-m\left(2\right)\)

\(\left(1\right)-có-2ngo-phân-biệt\Leftrightarrow\left(2\right)có-2ngo-phân-biệt-thỏa:t\ge0\)

\(\Rightarrow f\left(0\right)=-3\)

\(\Rightarrow f\left(t\right)min=\dfrac{-\Delta}{4a}=-7\Leftrightarrow t=2\)

\(\Rightarrow-7< -m\le-3\Leftrightarrow3\le m< 7\)

\(\left(m^2-4\right)x=3m+6\Leftrightarrow\left(m^2-4\right)x-3m-6=0\) vô nghiệm 

\(\Leftrightarrow\left\{{}\begin{matrix}m^2-4=0\\-3m-6\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m=2\\m=-2\end{matrix}\right.\\m\ne-2\end{matrix}\right.\Leftrightarrow m=2\)

Đáp án C.

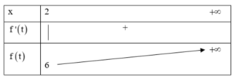
Bất phương trình ⇔ log 2 5 x - 1 1 + log 2 5 x - 1 ≥ m  

Đặt  t = log 2 5 x - 1 , do x ≥ 1 ⇒ t ∈ [ 2 ; + ∞ )  

Bất phương trình t 2 + t ≥ m ⇔ f ( t ) ≥ m  

Với  f ( t ) = t 2 + t , f ' ( t ) = 2 t + 1 > 0  với  t ∈ [ 2 ; + ∞ ) nên hàm số f ( t ) đồng biến nên min ( t ) = f ( 2 ) = 6  

Do đó theo bài ra để bất phương trình có nghiệm  x ≥ 1  thì m ≤ min   f ( t ) ⇔ m ≤ 6