Cho tứ diện ABCD có AB = 3a, AC = 5a, AD = 4a, các góc B A C ^ = D A C ^ = B A D ^ = 60 0 . Khi đó thể tích khối ABCD là:
A . 5 a 3 3
B . 5 a 3 2
C . a 3 2
D . 10 a 3 2
Những câu hỏi liên quan
Cho tứ diện ABCD có AB 3a, AC 5a, AD 4a, các góc
B
A
C
^
D
A
C
^
B
A
D
^
60
°
. Khi đó thể tích khối ABCD là: A.
5
a
3
3
B...
Đọc tiếp
Cho tứ diện ABCD có AB = 3a, AC = 5a, AD = 4a, các góc B A C ^ = D A C ^ = B A D ^ = 60 ° . Khi đó thể tích khối ABCD là:
A. 5 a 3 3
B. 5 a 3 2
C. a 3 2
D. 10 a 3 2
Cho tứ diện ABCD có
A
B
3
a
, AC 5a, AD 4a, các góc
B
A
C
^
D
A
C
^
B
A
D
^
60
°
. Khi đó thể tích khối ABCD là: A.
5
a...
Đọc tiếp
Cho tứ diện ABCD có A B = 3 a , AC = 5a, AD = 4a, các góc B A C ^ = D A C ^ = B A D ^ = 60 ° . Khi đó thể tích khối ABCD là:
A. 5 a 3 3
B. 5 a 3 2
C. a 3 2
D. 10 a 3 2
Đáp án B.
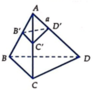
Gọi B’, C’, D’ lần lượt thuộc AB, AC, AD sao cho A B ' = A C ' = A D ' = a
Tứ diện AB’C’D’ là tứ diện đều cạnh a ⇒ V A B ' C ' D ' = a 3 2 12 (công thức cần nhớ)
Mà
V A B C D V A B ' C ' D ' = A B A B ' . A C A C ' . A D A D ' = 3.4.5 ⇒ V A B C D = 12.5. V A B ' C ' D ' = 5 a 3 2
Đúng 1
Bình luận (0)
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau; AB 3a, AC 4a, AD5a. Gọi M, N, P lần lượt là trọng tâm của tam giác DAB, DBC, DCA. Tính thể tích của khối chóp DMNA theo a. A.
V
10
a
3
27
B.
V...
Đọc tiếp
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau; AB =3a, AC = 4a, AD=5a. Gọi M, N, P lần lượt là trọng tâm của tam giác DAB, DBC, DCA. Tính thể tích của khối chóp DMNA theo a.
A. V = 10 a 3 27
B. V = 80 a 3 27
C. V = 20 a 3 27
D. V = 40 a 3 27
Đáp án C
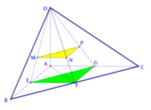
Gọi E,F,G lần lượt là trung điểm của các cạnh AB, BC, AC.
Khi đó:
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau; AB 3a, AC 4a, AD 5a. Gọi M, N, P lần lượt là trọng tâm của tam giác DAB, DBC, DCA. Tính thể tích của khối chóp DMNA theo a. A.
V
10
a
3
27
B.
V
80
a
3
27
C....
Đọc tiếp
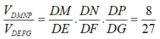
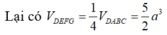
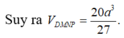
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau; AB = 3a, AC = 4a, AD = 5a. Gọi M, N, P lần lượt là trọng tâm của tam giác DAB, DBC, DCA. Tính thể tích của khối chóp DMNA theo a.
A. V = 10 a 3 27
B. V = 80 a 3 27
C. V = 20 a 3 27
D. V = 40 a 3 27
Đáp án C
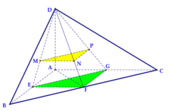
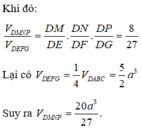
Gọi E,F,G lần lượt là trung điểm của các cạnh AB, BC, AC
Đúng 0
Bình luận (0)
Cho hình tứ diện ABCD có AD vuông góc với mặt phẳng (ABC), tam giác ABC có
A
B
3
a
,
A
C
4
a
,
B
C
5
a
. Tính góc giữa hai mặt phẳng (ABC) và (DBC), biết khối tứ diện ABCD có thể tích bằng
24
3
a
3
15
. A....
Đọc tiếp
Cho hình tứ diện ABCD có AD vuông góc với mặt phẳng (ABC), tam giác ABC có A B = 3 a , A C = 4 a , B C = 5 a . Tính góc giữa hai mặt phẳng (ABC) và (DBC), biết khối tứ diện ABCD có thể tích bằng 24 3 a 3 15 .
A. 30°
B. 45°
C. 60°
D. 90°
Đáp án A.
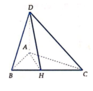
Từ dữ liệu đề bài ta thấy A B 2 + A C 2 = B C 2 ⇒ tam giác ABC vuông tại A.
Trong mặt phẳng A B C kẻ A H ⊥ B C tại H.
Ta có D A ⊥ B C A H ⊥ B C D A ∈ D A H ; A H ∈ D A H D A ∩ A H = A ⇒ D H ⊥ B C (định lý ba đường vuông góc).
Ta có A B C ∩ D B C = B C A H ⊥ B C ; D H ⊥ B C A H ∈ A B C ; D H ∈ D B C ⇒ A B C , D B C ^ = A H D ^ .
Ta có A H = A B . A C B C = 3 a .4 a 5 a = 12 a 5 .
Tam giác ADH vuông tại A.
⇒ tan A H D ^ = D A A H = 3. V A B C D S A B C 12 a 5 = 3.24 3 a 3 15. 1 2 .3 a .4 a 12 a 5 = 3 3
⇒ A H D ^ = 30 °
Vậy ta chọn A.
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có AB3a, AC4a,AD5a. Gọi M,N,P lần lượt là trọng tâm các tam giác DAB, DBC,DCA. Tính thể tích V của tứ diện DMNP khi thể tích tứ diện BACD đạt giá trị lớn nhất. A.
V
120
a
3
27
B.
V
+
10
a...
Đọc tiếp
Cho tứ diện ABCD có AB=3a, AC=4a,AD=5a. Gọi M,N,P lần lượt là trọng tâm các tam giác DAB, DBC,DCA. Tính thể tích V của tứ diện DMNP khi thể tích tứ diện BACD đạt giá trị lớn nhất.
A. V = 120 a 3 27
B. V + 10 a 3 4
C. V = 80 a 3 7
D. V = 20 a 3 27
Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau, AB 6a, AC 5a, AD 4a. Gọi M, N, P tương ứng là trung điểm của các cạnh BC, CD, DB. Thể tích V của tứ diện AMNP là:
Đọc tiếp
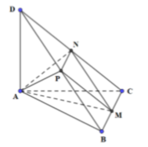
Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau, AB = 6a, AC = 5a, AD = 4a. Gọi M, N, P tương ứng là trung điểm của các cạnh BC, CD, DB. Thể tích V của tứ diện AMNP là:
Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau,
A
B
6
a
,
A
C
5
a
,
A
D
4
a
.
Gọi M, N, P tương ứng là trung điểm của các cạnh BC, CD, DB. Thể tích V của tứ diện AMNP là: A.
V
5...
Đọc tiếp
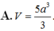
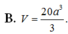
Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau, A B = 6 a , A C = 5 a , A D = 4 a . Gọi M, N, P tương ứng là trung điểm của các cạnh BC, CD, DB. Thể tích V của tứ diện AMNP là:
A. V = 5 a 3 3 .
B. V = 20 a 3 3 .
C. V = 5 a 3
D. V = 10 a 3
Chọn C.
Phương pháp:
+) Thể tích khối tứ diện OABC có OA, OB, OC đôi một vuông góc và có độ dài các cạnh đó lần lượt là a, b, c là: V = 1 6 a b c
Cách giải:
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có tam giác BCD vuông tại B, AC vuông góc với mặt phẳng (BCD),
A
C
5
a
,
B
C
3
a
,
B
D
4
a
. Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD A.
R
5
a
3
2
B.
R...
Đọc tiếp
Cho tứ diện ABCD có tam giác BCD vuông tại B, AC vuông góc với mặt phẳng (BCD), A C = 5 a , B C = 3 a , B D = 4 a . Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD
A. R = 5 a 3 2
B. R = 5 a 2 3
C. R = 5 a 3 3
D. R = 5 a 2 2
Đáp án D
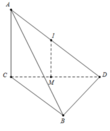
Gọi M là trung điểm của CD đường thẳng qua M song song với AC cắt AD tại trung điểm I của AD. Khi đó I là tâm mặt cầu ngoại tiếp khối tứ diện
Đúng 0
Bình luận (0)