Đáp án C
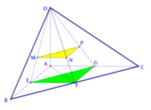
Gọi E,F,G lần lượt là trung điểm của các cạnh AB, BC, AC.
Khi đó:
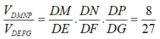
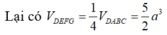
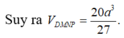
Đáp án C

Gọi E,F,G lần lượt là trung điểm của các cạnh AB, BC, AC.
Khi đó:
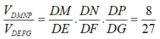
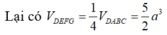
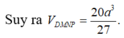
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau, biết rằng AB = a; AC =a 2 ; AD = a 3 ,(a>0) Thể tích V của khối tứ diện ABCD là:
A. V = a 3 6 3
B. V = a 3 6 6
C. V = a 3 6 2
D. V = a 3 6 9
Cho tứ diện ABCD có AB,AC,AD đôi một vuông góc với nhau, AB=a, AC=b, AD=c Tính thể tích V của khối tứ diện ABCD theo a, b, c
![]()
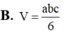
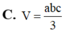
![]()
Cho tứ diện ABCD có các cạnh BA, BC, BC đôi một vuông góc với nhau, BA = 3a, BC = BD = 2a. Gọi M và N lần lượt là trung điểm của AB và AD. Tính thể tích khối chóp C.BDNM
A. V = 8 a 3
B. V = 2 a 3 3
C. V = 3 a 3 2
D. V = a 3
Cho tứ diện (ABCD) có các cạnh AB, AC, AD đôi một vuông góc với nhau, AB = 6a, AC= 7a, AD = 8a . Gọi M, N, P lần lượt là trung điểm của BC, CD, BD Thể tích khối tứ diện AMNP là:
A. 14 a 2 .
B. 28 a 2 .
C. 42 a 2 .
D. 7 a 2 .
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD). Góc giữa mặt phẳng (SBC) và (ABCD) bằng 45 0 . Gọi M, N lần lượt là trung điểm của AB, AD. Tính thể tích khối chóp S.CDMN theo a
A . 5 a 3 8
B . a 3 8
C . 5 a 3 24
D . a 3 3
Cho tứ diện đều ABCD có cạnh bằng 3. Gọi M, N lần lượt là trung điểm các cạnh AD, BD. Gọi P là điểm trên cạnh AB sao cho 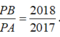 . Tính thể tích V của khối tứ diện PMNC
. Tính thể tích V của khối tứ diện PMNC
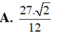

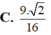

Cho khối tứ diện đều ABCD cạnh bằng Gọi M, N, P lần lượt là trọng tâm của ba tam giác ABC, ABD, ACD. Tính thể tích V của khối chóp AMNP.
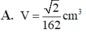
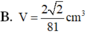

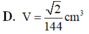
Cho hình chóp SABCD có đáy là hình chữ nhật tâm O,AB=a,AD=a căn 3 , tam giác SAD đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M là trung điểm SA, G là trọng tâm tam giác SCD, Thể tích khối tứ diện DOGM bằng
Cho hình chóp đều S.ABCD, có cạnh đáy bằng 2a. Mặt bên hình chóp tạo với đáy một góc bằng 60 0 . Mặt phẳng (P) chứa AB đi qua trọng tâm G của tam giác SAC cắt SC, SD lần lượt tại M, N. Tính theo a thể tích V khối chóp S.ABMN.
A. V = 3 a 3
B. V = 3 4 a 3
C. V = 3 2 a 3
D. V = 3 3 2 a 3