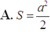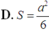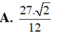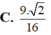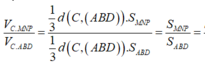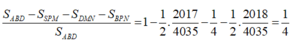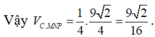Các câu hỏi tương tự
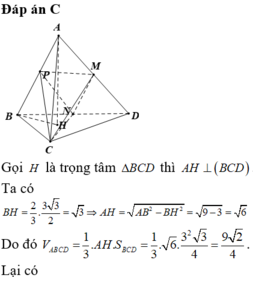
Cho tứ diện ABCD đều cạnh bằng 1. Gọi M, N lần lượt là trung điểm các cạnh AB, BC. Điểm P trên cạnh CD sao cho Mặt phẳng (MNP) cắt cạnh AD tại Q. Thể tích của khối đa diện BMNPQD bằng A.
11
2
216
B.
2
27
C. ...
Đọc tiếp
Cho tứ diện ABCD đều cạnh bằng 1. Gọi M, N lần lượt là trung điểm các cạnh AB, BC. Điểm P trên cạnh CD sao cho Mặt phẳng (MNP) cắt cạnh AD tại Q. Thể tích của khối đa diện BMNPQD bằng
A. 11 2 216
B. 2 27
C. 5 2 108
D. 7 2 216
Cho tứ diện đều ABCD có cạnh bằng a, trên các cạnh AB, AC, AD lần lượt lấy các điểm M, N, P sao cho AB 2 AM, AN 2NC, AD 2 AP. Thể tích của khối tứ diện AMNP là: A.
a
3
2
72
B.
a
3
3
48
C. ...
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng a, trên các cạnh AB, AC, AD lần lượt lấy các điểm M, N, P sao cho AB = 2 AM, AN= 2NC, AD = 2 AP. Thể tích của khối tứ diện AMNP là:
A. a 3 2 72
B. a 3 3 48
C. a 3 2 48
D. a 3 2 12
Cho tứ diện (ABCD) có các cạnh AB, AC, AD đôi một vuông góc với nhau, AB 6a, AC 7a, AD 8a . Gọi M, N, P lần lượt là trung điểm của BC, CD, BD Thể tích khối tứ diện AMNP là: A. 14
a
2
. B. 28
a
2
. C. 42
a
2
. D. 7
a
2...
Đọc tiếp
Cho tứ diện (ABCD) có các cạnh AB, AC, AD đôi một vuông góc với nhau, AB = 6a, AC= 7a, AD = 8a . Gọi M, N, P lần lượt là trung điểm của BC, CD, BD Thể tích khối tứ diện AMNP là:
A. 14 a 2 .
B. 28 a 2 .
C. 42 a 2 .
D. 7 a 2 .
Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M, N là hai điểm thay đổi lần lượt thuộc cạnh BC, BD sao cho mặt phẳng (AMN) luôn vuông góc với mặt phẳng (BCD) Gọi
V
1
,
V
2
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của thể tích khối tứ diện ABMN. Tính
V
1
+
V
2
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M, N là hai điểm thay đổi lần lượt thuộc cạnh BC, BD sao cho mặt phẳng (AMN) luôn vuông góc với mặt phẳng (BCD) Gọi V 1 , V 2 lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của thể tích khối tứ diện ABMN. Tính V 1 + V 2
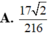
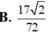
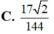
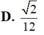
Cho tứ diện ABCD có các cạnh BA, BC, BC đôi một vuông góc với nhau, BA 3a, BC BD 2a. Gọi M và N lần lượt là trung điểm của AB và AD. Tính thể tích khối chóp C.BDNM A. V 8
a
3
B. V
2
a
3
3
C. V
3
a
3
2
D. V...
Đọc tiếp
Cho tứ diện ABCD có các cạnh BA, BC, BC đôi một vuông góc với nhau, BA = 3a, BC = BD = 2a. Gọi M và N lần lượt là trung điểm của AB và AD. Tính thể tích khối chóp C.BDNM
A. V = 8 a 3
B. V = 2 a 3 3
C. V = 3 a 3 2
D. V = a 3
Cho hình lăng trụ ABC.ABC có thể tích bằng V. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC’, BB’. Thể tích của khối tứ diện CMNP bằng
Đọc tiếp
Cho hình lăng trụ ABC.A'B'C' có thể tích bằng V. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, A'C’, BB’. Thể tích của khối tứ diện CMNP bằng
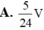
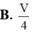
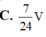
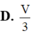
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a góc giữa mặt bên và mặt đáy bằng
60
o
Gọi M, N lần lượt là trung điểm của các cạnh cạnh SD, DC. Thể tích khối tứ diện ACMN là
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a góc giữa mặt bên và mặt đáy bằng 60 o Gọi M, N lần lượt là trung điểm của các cạnh cạnh SD, DC. Thể tích khối tứ diện ACMN là
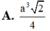
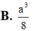
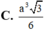
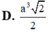
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, góc giữa mặt bên và mặt đáy bằng
60
o
. Gọi M, N lần lượt là trung điểm của các cạnh cạnh SD, DC. Thể tích khối tứ diện ACMN là
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, góc giữa mặt bên và mặt đáy bằng 60 o . Gọi M, N lần lượt là trung điểm của các cạnh cạnh SD, DC. Thể tích khối tứ diện ACMN là
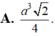
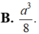
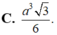
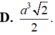
Cho tứ diện đều ABCD có cạnh bằng a. Gọi E,F lần lượt là các điểm đối xứng của B qua C,D và M là trung điểm của đoạn thẳng AB. Gọi (T) là thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MEF). Tính diện tích S của thiết diện (T)
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng a. Gọi E,F lần lượt là các điểm đối xứng của B qua C,D và M là trung điểm của đoạn thẳng AB. Gọi (T) là thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MEF). Tính diện tích S của thiết diện (T)