Đáp án B.
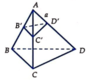
Gọi B’, C’, D’ lần lượt thuộc AB, AC, AD sao cho AB' = AC' = AD' = a
=> Tứ diện AB’C’D’ là tứ diện đều cạnh a
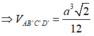
(công thức cần nhớ)
Mà
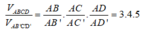
![]()
Đáp án B.

Gọi B’, C’, D’ lần lượt thuộc AB, AC, AD sao cho AB' = AC' = AD' = a
=> Tứ diện AB’C’D’ là tứ diện đều cạnh a
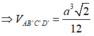
(công thức cần nhớ)
Mà
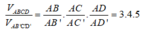
![]()
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau, biết rằng AB = a; AC =a 2 ; AD = a 3 ,(a>0) Thể tích V của khối tứ diện ABCD là:
A. V = a 3 6 3
B. V = a 3 6 6
C. V = a 3 6 2
D. V = a 3 6 9
Cho tứ diện ABCD có AB,AC,AD đôi một vuông góc với nhau, AB=a, AC=b, AD=c Tính thể tích V của khối tứ diện ABCD theo a, b, c
![]()
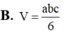
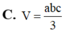
![]()
Cho tứ diện ABCD có AD ⊥ (ABC), ABC là tam giác vuông tại B. Biết
BC=A, AB=a 3 , AD=3a Quay các tam giác ABC và ABD xung quanh đường thẳng AB ta được 2 khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng
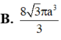
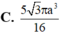
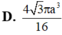
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau; AB =3a, AC = 4a, AD=5a. Gọi M, N, P lần lượt là trọng tâm của tam giác DAB, DBC, DCA. Tính thể tích của khối chóp DMNA theo a.
A. V = 10 a 3 27
B. V = 80 a 3 27
C. V = 20 a 3 27
D. V = 40 a 3 27
Cho hình hộp ABCD A B C D . A'B C'D ' có :
AB=1, AD=2, A A'=3. Góc BAD =120 độ, BAA= 60 độ , DAA=60 độ . Gọi I là giao điểm của BC' và BC' . 1) Tính các tích sau AB .AD ,AB. AA' ,AD. AA'. 2) Tính AI AC . 3) Tính AI . 4) Tính góc giữa AI và AC'.Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC), AC=AD=4,AB=3, BC=5 Tính khoảng cách d từ điểm A đến mặt phẳng (BCD).
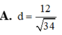
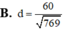
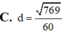
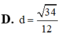
Bài 10. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, cạnh bên bằng a * sqrt(3) . O là tâm hình vuông 1/ Chứng minh :a) (SAC) I (ABCD) b) (SAC) (SBD). 2 / a ) Tính d(S; (ABCD)) b) Tính d(O; (SCD)) 3/ Tính góc giữa:a) SC và (ABCD); b) (SAB) và (ABCD).
Cho tứ diện đều ABCD có cạnh bằng a, trên các cạnh AB, AC, AD lần lượt lấy các điểm M, N, P sao cho AB = 2 AM, AN= 2NC, AD = 2 AP. Thể tích của khối tứ diện AMNP là:
A. a 3 2 72
B. a 3 3 48
C. a 3 2 48
D. a 3 2 12
Cho tứ diện ABCD có AB ⊥ (BCD) và AB=a√3, BCD là tam giác đều cạnh a.Tính góc giữa: 1) AC và (BCD) 2) AD và (BCD) 3) AD và (ABC)