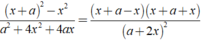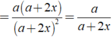Rút gọn các biểu thức sau ( x + a ) 2 - x 2 a 2 + 4 x 2 + 4 a x

Những câu hỏi liên quan
Rút gọn các biểu thức sau : a)(x^2-3)/(x+căn3)
ĐKXĐ: `x>=0;x\ne9`
`(x^2-3)/(sqrtx-3)=((x-sqrt3)(x+sqrt3))/(x+sqrt3)=x-sqrt3`
Đúng 2
Bình luận (1)
`a)(x^2-3)/(x+\sqrt3)`
`->` ĐKXĐ : `x>=0;x\ne9`
`=((x-\sqrt3)(x+\sqrt3))/(x+\sqrt3)`
`=(x-\sqrt3)/1`
`=x-\sqrt3`
Đúng 2
Bình luận (2)
rút gọn các biểu thức sau: a, A= |-4|+|6x|+2 khi x= 2
Rút gọn các biểu thức sau
(
x
+
a
)
2
-
x
2
a
2
+
4
x
2
+
4
a
x
Đọc tiếp
Rút gọn các biểu thức sau ( x + a ) 2 - x 2 a 2 + 4 x 2 + 4 a x
Tìm x để các biểu thức sau có nghĩa và rút gọn các biểu thức sau: a) x-√x /√x-1 - x-1/√x+1
\(\dfrac{x-\sqrt{x}}{\sqrt{x}-1}-\dfrac{x-1}{\sqrt{x}+1}\);\(ĐK:x\ge0;x\ne1\)
\(\Leftrightarrow\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}-\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\)
\(\Leftrightarrow\sqrt{x}-\left(\sqrt{x}-1\right)\)
\(\Leftrightarrow\sqrt{x}-\sqrt{x}+1\)
\(\Leftrightarrow1\)
Đúng 2
Bình luận (0)
a: \(=\sqrt{x}\cdot\dfrac{\left(\sqrt{x}-1\right)}{\sqrt{x}-1}-\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\)
\(=\sqrt{x}-\sqrt{x}+1=1\)
Đúng 2
Bình luận (0)
a) rút gọn biểu thức
A = 5 ( x + 1 )2 - 3 ( x -3 )2 - 4 ( x + 2 ) ( x - 2 )
b) rút gọn các biểu thức sau và tính giá trị của biểu thức tại x = -7
B = ( 2x - 3 ) ( 3x + 5 ) - 2x ( x - 2 )2 - ( 2x - 3 ) ( 2x + 3 )
`Answer:`
`a)`
`A=5(x+1)^2-3(x-3)^2-4(x^2-4)`
`=>A=5(x^2+2x+1)-3(x^2-6x+9)-4x^2+16`
`=>A=5x^2+10x+5-3x^2+18x-27-4x^2+16`
`=>A=(5x^2-3x^2-4x^2)+(10x+18x)+(5-27+16)`
`=>A=-2x^2+28x-6`
`b)`
`B=5(x+1)^2-3(x-3)^2-4(x+2)(x-2)`
`=2x(3x+5)-3(3x+5)-2x(x^2-4x+4)-[(2x)^2-3^2]`
`=6x^2+10x-9x-15-2x^3+8x^2-8x-4x^2+9`
`=(6x^2-4x^2+8x^2)-2x^3+(10x-9x-8x)+(-15+9)`
Thay `x=-7` vào ta được:
`B=10(-7)^2-2(-7)^3-7(-7)-6`
`=>B=10.49-2(-343)+49-6`
`=>B=490+686+49-6`
`=>B=1219`
Rút gọn các biểu thức sau:
a) ( x + 2 )( x - 2 ) - ( x - 3 )(x + 1 )
a, ( x+ 2 )( x - 2 ) - ( x-3 ( x-1)
= \(^{x^2}\) - \(2^2\) - ( \(x^2\)+ x - 3x - x)
= \(x^2\) - 4 - \(x^2\) - x + 3x + 3
= 2x -1
Đúng 0
Bình luận (0)
a) \(\left(x+2\right)\left(x-2\right)-\left(x-3\right)\left(x+1\right)\)
\(=x^2-2^2-\left(x^2+x-3x-x\right)\)
\(=x^2-4-x^2-x+3x+3\)
\(=2x-1\)
Đúng 0
Bình luận (0)
Rút gọn các biểu thức sau a)(căn1-4a+4a^2 ) -2a b)x-2y-căn x^2-4xy+4y^2
a) \(\sqrt[]{1-4a+4a^2}\)
\(=\sqrt[]{\left(1-2a\right)^2}\)
\(=\left|1-2a\right|\)
\(=\left[{}\begin{matrix}1-2a\left(a\le\dfrac{1}{2}\right)\\2a-1\left(a>\dfrac{1}{2}\right)\end{matrix}\right.\)
b) \(x-2y-\sqrt[]{x^2-4xy+4y^2}\)
\(=x-2y-\sqrt[]{\left(x-2y\right)^2}\)
\(=x-2y-\left|x-2y\right|\)
\(=\left[{}\begin{matrix}x-2y-x+2y\left(x\ge2y\right)\\x-2y+x-2y\left(x< 2y\right)\end{matrix}\right.\)
\(=\left[{}\begin{matrix}0\left(x\ge2y\right)\\2x-4y\left(x< 2y\right)\end{matrix}\right.\)
\(=\left[{}\begin{matrix}0\left(x\ge2y\right)\\2\left(x-2y\right)\left(x< 2y\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
1 a. Rút gọn biểu thức sau A = \(\left(x^{\text{2}}-2x+4\right):\left(x^3+8\right)-x^2\) rồi tính giá trị của A tại x = -2
b. Rút gọn biểu thức B = (x - 2) : 2x + 5x rồi tính giá trị của biểu thức B tại x = 0
Rút gọn các biểu thức sau:
\(\sqrt{x}-2+\dfrac{10-x}{\sqrt{x}+2}\)
Lời giải:
ĐKXĐ: $x\geq 0$
$=\frac{(\sqrt{x}-2)(\sqrt{x}+2)+10-x}{\sqrt{x}+2}=\frac{x-4+10-x}{\sqrt{x}+2}=\frac{6}{\sqrt{x}+2}$
Đúng 1
Bình luận (0)