Với giá trị thực nào của a thì hệ phương trình x + y = a 2 + a + 1 x - y = - a 2 + a - 1 có nghiệm (x;y) với 3x+y nhỏ nhất?
A. a = - 5 2
B. a = 3 2
C. a = - 3 2
D. a = 0
Cho hệ phương trình: \(\hept{\begin{cases}kx-y=5\\x+y=1\end{cases}}\)
a/Với giá trị nào của k thì hệ phương trình có nghiệm là \(\left(x;y\right)=\left(2;-1\right)\)
b/Với giá trị nào của k thì hệ phương trình có nghiệm duy nhất?hệ phương trình vô nghiệm?
a) Ta có hệ phương trình \(\hept{\begin{cases}kx-y=5\\x+y=1\end{cases}}\) Thay nghiệm \(\left(x,y\right)=\left(2,-1\right)\) ta có hệ mới là :
\(\hept{\begin{cases}2k-1=5\\2-1=1\end{cases}\Leftrightarrow k=3}\)
b) Ta có : \(\hept{\begin{cases}kx-y=5\\x+y=1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=1-x\\kx-1-x=5\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=1-x\\x\left(k-1\right)=6\end{cases}}\)
Để hệ phương trình có nghiệm duy nhất : \(\Leftrightarrow k-1\ne0\) \(\Leftrightarrow k\ne1\)
Để hệ phương trình vô nghiệm \(\Leftrightarrow k-1=0\Leftrightarrow k=1\)
P/s : Em chưa học lớp 9 nên không biết cách trình bày cho lắm :))
cho hệ phương trình mx -y =2m 4x - my=6+m Với giá trị nào của m thì hệ phương trình có duy nhất một nghiệm Với giá trị nào của m thì hệ phương trình có vô số nghiệm Với giá trị nào của m thì hệ phương trình vô nghiệm
a: Để hệ có duy nhất 1 nghiệm thì \(\dfrac{m}{4}< >\dfrac{-1}{-m}=\dfrac{1}{m}\)
=>m^2<>4
=>m<>2 và m<>-2
b: Để hệ có vô số nghiệm thì \(\dfrac{m}{4}=\dfrac{-1}{-m}=\dfrac{2m}{m+6}=\dfrac{1}{m}\)
=>m^2=4 và 2m^2=m+6
=>m=2
c: Để hệ vô nghiệm thì m/4=1/m<>2m/m+6
=>m=-2
Với giá trị nào của a thì hệ phương trình x + y = 1 x - y = 2 a - 1 có nghiệm (x;y) với x.y lớn nhất?
A. a = 1 4
B. a = 1 2
C. a = - 1 2
D. a = 1
Ta có : x + y = 1 x - y = 2 a - 1 ⇔ x + y = 1 2 x = 2 a ⇔ y = 1 - a x = a
Do đó :
x y = a . 1 - a = a - a 2 = - a 2 - 2 . 1 2 a + 1 4 + 1 4 = - a - 1 2 2 + 1 4
Do - a - 1 2 2 ≤ 0 ∀ a ⇒ - a - 1 2 2 + 1 4 ≤ 1 4
Suy ra,giá trị lớn nhất của xy là 1 4 khi a = 1 2 .
Đáp án là B.
1.Cho hpt \(\hept{\begin{cases}nx-y=4\\x+y=1\end{cases}}\)
a) Với giá trị nào của n thì hệ phương trình có duy nhất nghiệm?
b) Với giá trị nào của n thì hệ phương trình vô nghiệm
Bài 3: Cho hệ phương trình \(\hept{\begin{cases}3x+my=4\\x+y=1\end{cases}}\)
a. Tìm m để hệ phương trình trên có nghiệm duy nhất, vô số nghiệm
b. Tìm m để hệ phương trình trên có nghiệm x<0, y>0
1:
a)\(\hept{\begin{cases}nx+x=5
\\x+y=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x.\left(n+1\right)=5\left(1\right)\\x+y=1\end{cases}}\)
Cho hệ pt: \(\left\{{}\begin{matrix}3x-y=2\\9x-my=m\end{matrix}\right.\)
1. Với giá trị nào của m thì hệ phương trình vô nghiệm
2. Với giá trị nào của m thì hệ phương trình có vô số nghiệm?
3. Với giá trị nào của m thì hệ phương trình có nghiệm duy nhất
4. Tìm m để hệ có nghiệm duy nhất x> 0; y<0
cho hệ phương trình x-y+m=0 và (x+y-2)(x-2y+1) với giá trị nào của m thì hệ phương trình có một nghiệm duy nhất
Với giá trị nào của a thì hệ phương trình:{x+ay=1và ax+y=2
a,có nghiệm duy nhất
b, vô nghiệm
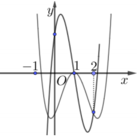
Cho hàm số y=f(x) là hàm đa thức hệ số thực. Hình vẽ bên là đồ thị của hai hàm số y=f(x) và y=f'(x) . Phương trình f(x)= m e x có hai nghiệm thực phân biệt thuộc đoạn [0;2] khi và chỉ khi m thuộc nửa khoảng [a;b). Giá trị của a+b gần nhất với giá trị nào dưới đây ?
A. 0,27.
B. −0,54.
C. −0,27.
D. 0,54.