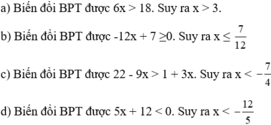Giải các bất phương trình mũ sau: 11 x + 6 ≥ 11 x

Những câu hỏi liên quan
Giải các bất phương trình sau và biểu diễn tập hợp nghiệm trên trục số
\(\dfrac{2x-3}{2}\)>\(\dfrac{8x-11}{6}\), 2x-3 ≤ 8x-11, \(\dfrac{x-3}{2}\)>\(\dfrac{x-11}{3}\)
\(\dfrac{2x-3}{2}>\dfrac{8x-11}{6}\)
\(\Leftrightarrow\dfrac{3\left(2x-3\right)}{6}>\dfrac{8x-11}{6}\)
\(\Leftrightarrow3\left(2x-3\right)>8x-11\)
\(\Leftrightarrow6x-9>8x-11\)
\(\Leftrightarrow-2x>-2\)
\(\Leftrightarrow x< 1\)
Vậy \(S=\left\{x|x< 1\right\}\)
Đúng 0
Bình luận (0)
\(2x-3\le8x-11\)
\(\Leftrightarrow-6x\le-8\)
\(\Leftrightarrow x\ge\dfrac{8}{6}\)
Vậy \(S=\left\{x|x\ge\dfrac{8}{6}\right\}\)
Đúng 0
Bình luận (0)
\(\dfrac{x-3}{2}>\dfrac{x-11}{3}\)
\(\Leftrightarrow\dfrac{3\left(x-3\right)}{6}>\dfrac{2\left(x-11\right)}{6}\)
\(\Leftrightarrow3\left(x-3\right)>2\left(x-11\right)\)
\(\Leftrightarrow3x-9>2x-22\)
\(\Leftrightarrow x>-13\)
Vậy \(S=\left\{x|x>-13\right\}\)
Đúng 0
Bình luận (0)
Giải các bất phương trình sau
a) 3x+2(5-x)>-11 b) 3x2-3x(-2+x)<36
a)3x+10-2x>-11
3x - 2x > -10-11
1x > -21
x > -21
b) 3x2 - 6x + 3x2 < 36
-6x < 36
x < -6
Đúng 0
Bình luận (0)
Giải các bất phương trình sau
a) 3x-8 > 5x +7
b) (11-x)(11+x) > 0
c) (x+2)(x+3) < 0
a, -2x>15 x>-15/2 c, th1 x+2>0 vs x+3 <0 suy ra x>-2 vs x<-3 . th2 x+2<0,x+3>0 suy ra x<-2 ,x>-3
b, 112-x2>0
x2<112 x<11
Đúng 0
Bình luận (0)
a) \(3x-8>5x+7\)
\(\Leftrightarrow-8>5x+7-3x\)
\(\Leftrightarrow-8>2x+7\)
\(\Leftrightarrow-8-7>2x\)
\(\Leftrightarrow-15>2x\)
\(\Leftrightarrow-\frac{15}{2}>x\)
\(\Rightarrow x< -\frac{15}{2}\)
b) \(\left(11-x\right)\left(11+x\right)>0\)
\(\Leftrightarrow x=\pm11\)
\(\Rightarrow-11< x< 11\)
c) \(\left(x+2\right)\left(x+3\right)< 0\)
\(\Leftrightarrow x=-2;-3\)
\(\Rightarrow-3< x< -2\)
Đúng 0
Bình luận (0)
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số: a, 3x -11 >5 -x
\(a,3x-11>5-x\\ \Leftrightarrow3x+x>5+11\\ \Leftrightarrow4x< 16\\ \Leftrightarrow x>4\)
Vậy bất phương trình có nghiệm là: \(S=\left\{x|x>4\right\}\)
biểu diễn
Đúng 1
Bình luận (0)
Giải các bất phương trình mũ sau:
4
x
-
2
x
+
1
+
8
2
1
-
x
8
x
Đọc tiếp
Giải các bất phương trình mũ sau: 4 x - 2 x + 1 + 8 2 1 - x < 8 x
2 2 x - 2 . 2 x + 8 < 2 3 x . 2 1 - x ⇔ 2 2 x + 2 . 2 x - 8 > 0
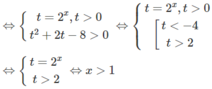
Đúng 0
Bình luận (0)
Bài 1: Giải các bất phương trình và phương trình sau :
a) 2(3-4x) = 10-(2x – 5)
Giải các bất phương trình và phương trình sau :
a) 3(2-4x) = 11-(3x – 1)
Bài 1:
a) Ta có: \(2\left(3-4x\right)=10-\left(2x-5\right)\)
\(\Leftrightarrow6-8x-10+2x-5=0\)
\(\Leftrightarrow-6x+11=0\)
\(\Leftrightarrow-6x=-11\)
hay \(x=\dfrac{11}{6}\)
b) Ta có: \(3\left(2-4x\right)=11-\left(3x-1\right)\)
\(\Leftrightarrow6-12x-11+3x-1=0\)
\(\Leftrightarrow-9x-6=0\)
\(\Leftrightarrow-9x=6\)
hay \(x=-\dfrac{2}{3}\)
Đúng 2
Bình luận (0)
Giải các phương trình sau:
2
(
x
+
5
)
3
+
x
+
12
2
-
5
(
x
-
2
)
6
x
3
+
11
Đọc tiếp
Giải các phương trình sau: 2 ( x + 5 ) 3 + x + 12 2 - 5 ( x - 2 ) 6 = x 3 + 11
Ta có:
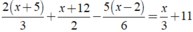
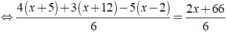
⇔ 4x + 20 + 3x + 36 - 5x + 10 = 2x + 66
⇔ 0x = 0
⇒ Phương trình đã cho vô số nghiệm.
Vậy phương trình đã cho vô số nghiệm.
Đúng 0
Bình luận (0)
Giải các bất phương trình mũ sau: 16 x - 4 x - 6 ≤ 0
Đặt t = 4 x (t > 0), ta có hệ bất phương trình:
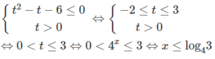
Đúng 0
Bình luận (0)
Giải các bất phương trình sau:a)
2
x
−
7
11
−
4
x
;
b)
x
−
2
2
−
x
2
−
8
x
+
3
≥
0
;
c)
2
3
−
3...
Đọc tiếp
Giải các bất phương trình sau:
a) 2 x − 7 > 11 − 4 x ; b) x − 2 2 − x 2 − 8 x + 3 ≥ 0 ;
c) 2 3 − 3 x − 6 2 > 1 + 3 x 6 ; d) x − 5 x + 1 + 4 x + 3 < − 5 x 2