Cho phương trình (2m - 1) x 2 - 2(m + 4)x + 5m + 2 = 0 ( m ≠ 1 2 )
Khi phương trình có nghiệm x 1 , x 2 hãy tính tổng S và tích P của hai nghiệm theo m
Cho phương trình (2m - 1) x 2 - 2(m + 4)x + 5m + 2 = 0 ( m ≠ 1 2 )
Tìm giá trị của m để phương trình có nghiệm.
Cho phương trình (2m -1)x2 -2(m + 4)x + 5m + 2 = 0. (3)
Tìm m để phương trình có nghiệm? Có 1 nghiệm? có nghiệm kép?
Bạn giải denta và chú ý điều kiện của a nhá
cho phương trình ẩn x: \(x^2-\left(2m+1\right)x+m^2+5m=0\)
a, giải phương trình với m = -2
b, tìm m để phương trình có hai nghiệm sao cho tích các nghiệm bằng 6
a, \(x^2-\left(2m+1\right)x+m^2+5m=0\)
Với m=2
\(x^2-\left[2.\left(-2\right)+1\right]x+\left(-2\right)^2+5.\left(-2\right)=0\)
\(x^2+3x-6=0\)
\(\Delta=3^2-4.1.\left(-6\right)\)
\(=9+24\)
\(=33>0\Rightarrow\sqrt{\Delta}=\sqrt{33}\)
\(\Rightarrow\)Phương trình có 2 nghiệm phân biệt:
\(x_1=\dfrac{-3+\sqrt{33}}{2}\)
\(x_2=\dfrac{-3-\sqrt{33}}{2}\)
Vậy khi m=-2 thì phương trình có nghiệm là \(x_1=\dfrac{-3+\sqrt{33}}{2};x_2=\dfrac{-3-\sqrt{33}}{2}\)
b,Ta có \(\Delta=\left[-\left(2m+1\right)\right]^2-4\left(m^2+5m\right)\)
\(=4m^2+4m+1-4m^2-20m\)
\(=1-16m\)
Phương trình có 2 nghiệm\(\Leftrightarrow\Delta\ge0\)
\(\Leftrightarrow1-16m\ge0\)
\(\Leftrightarrow m\le\dfrac{1}{16}\)
Khi đó hệ thức viet ta có tích các nghiệm là\(m^2+5m\)
Mà tích các nghiệm bằng 6, do đó \(m^2+5m=6\)
\(\Leftrightarrow m^2+5m-6=0\)
Ta thấy \(a+b+c=1+5+\left(-6\right)=0\) nên \(m_1=1;m_2=-6\)
Đối chiếu với điều kiện \(m\le\dfrac{1}{16}\) thì \(m=-6\) là giá trị cần tìm
-Chúc bạn học tốt-
a) Tìm m để phương trình\(\left(m+3\right)x^2-\left(m^2+5m\right)x+2m^2=0\) có nghiệm x=-2
tìm nghiệm còn lại
b Tìm m để phương trình \(\left(m^2-1\right)x^2-2mx+m^2+m+4=0\) có nghiệm x=2
Tìm nghiệm còn
lại?
b) Thay x=2 vào pt, ta được:
\(4\left(m^2-1\right)-4m+m^2+m+4=0\)
\(\Leftrightarrow4m^2-4-4m+m^2+m+4=0\)
\(\Leftrightarrow5m^2-3m=0\)
\(\Leftrightarrow m\left(5m-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=\dfrac{3}{5}\end{matrix}\right.\)
Áp dụng hệ thức Vi-et, ta được:
\(x_1+x_2=\dfrac{2m}{m^2-1}\)
\(\Leftrightarrow\left[{}\begin{matrix}x_2+2=0\\x_2+2=\dfrac{6}{5}:\left(\dfrac{36}{25}-1\right)=\dfrac{30}{11}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x_2=-2\\x_2=\dfrac{8}{11}\end{matrix}\right.\)
Cho phương trình (2m - 1) x 2 - 2(m + 4)x + 5m + 2 = 0 ( m ≠ 1 2 )
Tìm hệ thức giữa S và P sao cho trong hệ thức này không có m.
Phương trình (2m - 1) x 2 - 2(m + 4)x + 5m + 2 = 0 ( m ≠ 1 2 )
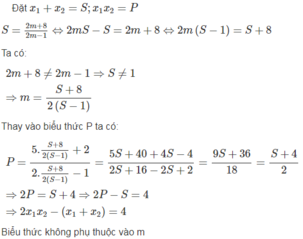
Cho phương trình ẩn x: x^2 – (5m – 1)x + 6m^2 – 2m = 0 (1)
a) Chứng minh rằng phương trình (1) luôn có nghiệm với mọi m.
b) Gọi x1, x2 là các nghiệm của (1). Tìm m để x1^2 + x2^2 = 1
a: \(\text{Δ}=\left(5m-1\right)^2-4\left(6m^2-2m\right)\)
\(=25m^2-10m+1-24m^2+8m=m^2-2m+1=\left(m-1\right)^2>=0\)
Do đó: Phương trình luôn có nghiệm
b: Theo đề, ta có: \(\left(x_1+x_2\right)^2-2x_1x_2=1\)
\(\Leftrightarrow\left(5m-1\right)^2-2\left(6m^2-2m\right)=1\)
\(\Leftrightarrow25m^2-10m+1-12m^2+4m-1=0\)
\(\Leftrightarrow13m^2-6m=0\)
=>m(13m-6)=0
=>m=0 hoặc m=6/13
Tìm giá trị của tham số m để phương trình sau vô nghiệm:\(\dfrac{x^2}{4}+\left(2m+1\right)x+5m^2+3m+16=0\)
Pt vô nghiệm khi:
\(\Delta=\left(2m+1\right)^2-\left(5m^2+3m+16\right)< 0\)
\(\Leftrightarrow-m^2+m-15< 0\) (luôn đúng)
Vậy pt đã cho vô nghiệm với mọi m
Bài 1: Tìm m để phương trình sau có 3 nghiệm lập thành 1 cấp số cộng:
1, \(x^3-x^2-m^2x+m^2=0\)
2, \((x-2)(x^2-2mx+2m+3)=0\)
3, \(x^3-(2m-3)x^2-mx+m-2=0\)
4, \(x^3+(2m-1)x^2+(4m+1)x+2m+3=0\)
Bài 2: Tìm m để phương trình sau có 4 nghiệm lập thành 1 cấp số cộng:
a, \(-x^4+2mx^2-2m+1=0\)
b, \(x^4+2(m-2)x^2+m^2-5m+5=0\)
Bài 3: Tìm 3 số lập thành 1 cấp số cộng biết tổng của chúng bằng tổng các bình phương bằng 83
Chứng tỏ rằng khi m thay đối, đường thẳng có phương trình luôn luôn đi qua một điểm cố định: (2m^2+m+4)x-(m²-m-1)y-5m^2-4m-13 = 0
Gọi \(A\left(x_0;y_0\right)\) là điểm cố định mà đường thẳng đã cho đi qua
\(\Rightarrow\) Với mọi m ta luôn có:
\(\left(2m^2+m+4\right)x_0-\left(m^2-m-1\right)y_0-5m^2-4m-13=0\)
\(\Leftrightarrow\left(2x_0-y_0-5\right)m^2+\left(x_0+y_0-4\right)m+4x_0+y_0-13=0\)
\(\Rightarrow\left\{{}\begin{matrix}2x_0-y_0-5=0\\x_0+y_0-4=0\\4x_0+y_0-13=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_0=3\\y_0=1\end{matrix}\right.\)
Vậy khi m thay đổi thì đường thẳng luôn đi qua điểm cố định có tọa độ \(\left(3;1\right)\)