Cho elip có phương trình: x 2 16 + y 2 4 = 1 . Gọi M là điểm thuộc E sao cho MF1= MF2. Khi đó tọa độ điểm M1; M2 là:
A.M1(0 ; 1) và M2(0; -1).
B. M1(0 ; 2) và M2(0; -2).
C. M1(0 ; 3) và M2(0; -3).
D. M1(0 ; 4) và M2(0; -4).
Cho Elip có phương trình \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{9} = 1\). Tìm tiêu điểm và tiêu cự của elip.
Ta có: \({a^2} = 36,{b^2} = 9 \Rightarrow c = \sqrt {36 - 9} = 3\sqrt 3 \) nên elip có hai tiêu điểm là \({F_1}\left( { - 3\sqrt 3 ;0} \right);{F_2}\left( {3\sqrt 3 ;0} \right)\) và tiêu cự là \({F_1}{F_2} = 2c = 6\sqrt 3 \).
Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\). Tìm các tiêu điểm và tiêu cự của elip.
Ta có: \(c = \sqrt {{{100}^2} - {{64}^2}} = 6\). Do đó (E) có hai tiêu điểm là \({F_1}\left( { - 6;0} \right),{F_2}\left( {6;0} \right)\) và có tiêu cự bằng 2c = 12.
Cho elip (E) có phương trình x²/16 + y²/9 =1. Viết phương trình đường thẳng (d) đi qua M(1;2) và cắt (E) tại A, B sao cho M là trung điểm AB
câu 1 trong các phương trình sau, phương trình nào là phương trình chính tắc của elip(vì sao)
a) x 2 9 + y 2 6 =1 b) x 2 25 + y 2 16 = 1
c) x 2 4 + y 2 9 =1 c) X 2 8 + y 2 2 =1
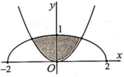
Cho (H) là hình phẳng giới hạn bởi parabol y = 3 2 x 2 và nửa đường elip có phương trình y = 1 2 4 - x 2 (với - 2 ≤ x ≤ 2 ) (phần tô đậm trong hình vẽ). Diện tích của (H) bằng:
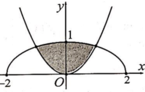
A. 2 π + 3 6
B. 2 π + 3 12
C. 2 π - 3 6
D. 4 π + 3 6
Chọn đáp án A
Phương trình hoành độ giao điểm của parabol y = 3 2 x 2 và nửa đường elip
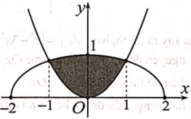
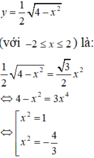
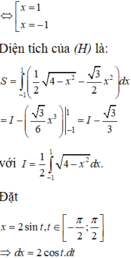
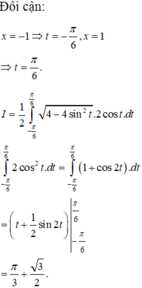
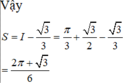
Cho (H) là hình phẳng giới hạn bởi parabol y = 3 2 x 2 và nửa đường elip có phương trình y = 1 2 4 - x 2 ( v ớ i - 2 ≤ x ≤ 2 ) (phần tô đậm trong hình vẽ). Diện tích của (H) bằng
A. 2 π + 3 6
B. 2 π + 3 12
C. 2 π - 3 6
D. 4 π + 3 6
Cho biết mỗi đường conic có phương trình dưới đây là đường conic dạng nào ( elip, hypebol, parabol) và tìm tọa độ tiêu điểm của đường conic đó.
a) \({y^2} = 18x\)
b) \(\frac{{{x^2}}}{{64}} + \frac{{{y^2}}}{{25}} = 1\)
c) \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{{16}} = 1\)
a) Đây là một parabol. Tiêu điểm của parabol có tọa độ là: \(F\left({\frac{9}{2};0} \right)\).
b) Đây là một elip. Tiêu điểm của elip có tọa độ là: \(\left\{ \begin{array}{l}{F_1}\left( { - \sqrt {{a^2} - {b^2}} ;0} \right) = \left( { - \sqrt {39} ;0} \right)\\{F_2}\left( {\sqrt {{a^2} - {b^2}} ;0} \right) = \left( {\sqrt {39} ;0} \right)\end{array} \right.\)
c) Đây là một hyperbol. Tiêu điểm của hypebol có tọa độ là: \(\left\{ \begin{array}{l}{F_1}\left( { - \sqrt {{a^2} + {b^2}} ;0} \right) = \left( { - 5;0} \right)\\{F_2}\left( {\sqrt {{a^2} + {b^2}} ;0} \right) = \left( {5;0} \right)\end{array} \right.\)
Phương trình nào sau đây là phương trình chính tắc của elip?
\(a)\frac{{{x^2}}}{{64}} + \frac{{{y^2}}}{{64}} = 1\)
b) \(\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{{64}} = 1\)
c) \(\frac{{{x^2}}}{{64}} + \frac{{{y^2}}}{{25}} = 1\)
d) \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{64}} = 1\)
Phương trình chính tắc của elip là: c) \(\frac{{{x^2}}}{{64}} + \frac{{{y^2}}}{{25}} = 1\).
a) Không là PTCT vì a =b =8
b) Không là PTCT
d) Không là PTCT vì a =5 < b =8.
Trong bản vẽ thiết kế, vòm của ô thoáng trong Hình 7.22 là nửa nằm phía trên trục hoành của elip có phương trình \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{4} = 1\). Biết rằng 1 đơn vị trên mặt phẳng toạ độ của bản vẽ thiết kế ứng với 30 cm trên thực tế. Tinh chiều cao h của ô thoáng tại điểm cách điểm chính giữa của đế ô thoáng 75 cm.
75 cm trên bản vẽ ứng với 2,5 đơn vị trên mặt phẳng tọa độ.
Gọi M là điểm trên vòm ô thoáng, có hoành độ 2,5 và tung độ là h.
M thuộc elip nên \(\frac{{2,{5^2}}}{{16}} + \frac{{{h^2}}}{4} = 1\)
\(\Leftrightarrow h = \sqrt {4.\left( {1 - \frac{{2,{5^2}}}{{16}}} \right)} = \frac{{\sqrt {39} }}{4} \approx 1,56\)
Vậy độ cao h trên thực tế là: \(h = 1,56.30 = 46,8\) cm
Phương trình nào sau đây là phương trình chính tắc của đường elip?
A. \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{9} = 1\)
B. \(\frac{{{x^2}}}{1} + \frac{{{y^2}}}{6} = 1\)
C. \(\frac{{{x^2}}}{4} - \frac{{{y^2}}}{1} = 1\)
D. \(\frac{{{x^2}}}{2} + \frac{{{y^2}}}{1} = 1\)