a: Xet ΔAHN và ΔCHM có

AH=CH

góc HAN=góc HCM

AN=CM

=>ΔAHN=ΔCHM

b: Xet ΔAHM và ΔBHN co

AH=BH

góc HAM=góc HBN

AM=BN

=>ΔAHM=ΔBHN

a) Sai

Sửa lại: "Đường thẳng Δ là đường thẳng vuông góc chung của hai đường thẳng chéo nhau a và b nếu Δ cắt cả a và b, đồng thời Δ ⊥ a và Δ ⊥ b"

b) Đúng

c) Đúng

d) Sai

Sửa lại: Đường thẳng đi qua M trên a và vuông góc với a, đồng thời cắt b tại N và vuông góc với b thì đó là đường vuông góc chung của a và b.

e) Sai.

Chọn A

Gọi (Q) là mặt phẳng đi qua M (2;2; -3) và song song với mặt phẳng (P).

Suy ra (Q):2x+y+z-3=0.

Do Δ // (P) nên Δ ⊂ (Q)).

D (N, Δ) đạt giá trị nhỏ nhất ó Δ đi qua N', với N' là hình chiếu của N lên (Q).

Gọi d là đường thẳng đi qua N và vuông góc (P),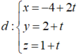 

Ta có N’ ∈ d => N' (-4+2t;2+t;1+t); N’ ∈ (Q) => t = 4/3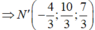

  cùng phương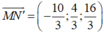 

Do |a|, |b| nguyên tố cùng nhau nên chọn 

Vậy  |a| + |b| + |c| = 15.

b) Xét tam giác ABF có:

BH là đường cao(AH⊥BH)

BH là phân giác( BC là phân giác \(\widehat{ABF}\))

=> Tam giác ABF cân tại B

=> AB=BF

Mà AB=CE(ΔMBA=ΔMCE)

=> CE=BF

c) Ta có: \(\widehat{ABC}=\widehat{BCE}\left(\Delta MBA=\Delta MCE\right)\)

Mà \(\widehat{ABC}=\widehat{KBC}\)(BC là phân giác \(\widehat{ABF}\))

\(\Rightarrow\widehat{BCE}=\widehat{KBC}\)

=> Tam giác KBC cân tại K

=> KM là đường trung tuyến cũng là đường phân giác \(\widehat{BKC}\left(1\right)\)

Ta có: KB=KC(KBC cân tại K), BF=CD(cmt)

=> KB-BF=KC-CE=> KF=KE

Xét tam giác BEK và tam giác CFK có:

KF=KE(cmt)

\(\widehat{K}\) chung

BK=KB(KBC cân tại K)

=> ΔBEK=ΔCFK(c.g.c)

=> \(\widehat{EBK}=\widehat{KCF}\)

Xét tam giác BFC và tam giác CEB có:

BC chung

\(\widehat{FBC}=\widehat{BCE}\)(cmt)

BF=CE(cmt)

=> ΔBFC=ΔCEB(c.g.c)

=> \(\widehat{BFC}=\widehat{BEC}\)

Xét tam giác BFI và tam giác CEI có:

\(\widehat{BFC}=\widehat{BEC}\left(cmt\right)\)

BF=CE(cmt)

\(\widehat{FBI}=\widehat{ECI}\left(cmt\right)\) 

=> ΔBFI=ΔCEI(g.c.g)

=> IF=IC

=> ΔIFK=ΔIEK(c.c.c)

=> KI là phân giác \(\widehat{BKC}\left(2\right)\)

\(\left(1\right),\left(2\right)\Rightarrow M,I,K\) thẳng hàng

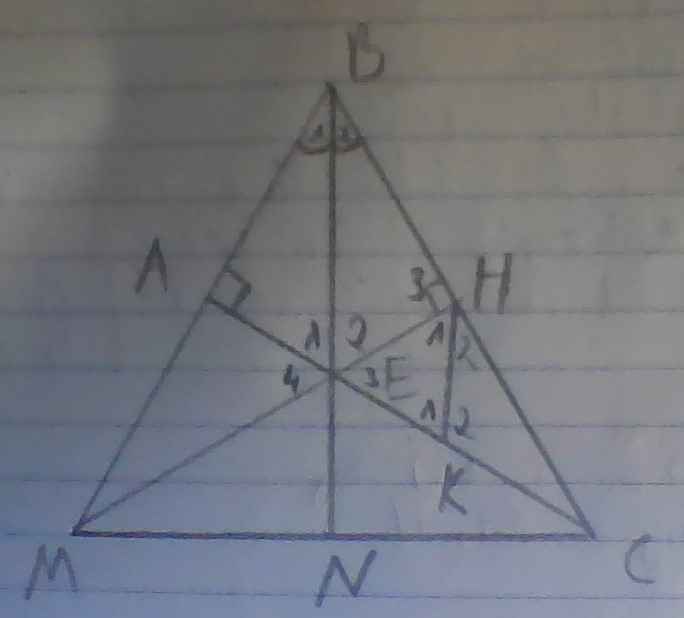
a) có BE là tia p/g của góc ABC

       => góc B₁ = góc B₂ = góc ABC/2 = 60⁰ /2 = 30⁰

  có △ABC vuông tại A => △ABE vuông tại A

         EH⊥BC=> △HBE vuông tại H

Xét △ vuông ABE và △vuông HBE có

             góc B₁ = góc B₂

                    BE chung

=>△ vuông ABE =△vuông HBE ( cạnh huyền - góc nhọn)

b) có △ABE vuông tại A=> góc B₁ + góc E₁ = 90⁰

                                         góc E₁ = 60⁰   ( vì góc B₁ = 30⁰)

có △ vuông ABE =△vuông HBE

    => góc E₁ = góc E₂ 

mà HK//BE => góc E₁ = góc K₁     (ĐV)

                       và góc E₂ = góc H₁ (SLT)

=> góc E₁ = góc E₂ = góc K₁=góc H₁ = 60⁰

 => △HEK đều

c) có góc E₁ = góc E₂ ; góc E₃ = góc E₄

  =>góc E₁ +góc E₄ = góc E₂ + góc E₃

=> góc BEM= góc BEC

Xét △BEM và △ BEC có

             góc B₁ = góc B₂

                   BE chung

          góc BEM= góc BEC

=> △BEM = △ BEC (g.c.g)

=>BM=BC

=>△BMC cân tại B

trong △BMC có BN là đường p/g xuất phát từ đỉnh B

lại có △BMC cân tại B

=> BN cũng là đường trung tuyến xuất phát từ đỉnh B

=> N là trung điểm của MC

=> NM=NC