Tìm số giao điểm n của đồ thị hàm số y = x 2 x 2 - 3 và đường thẳng y = 2
A. n = 8
B. n = 2
C. n = 6
D. n = 4
cho hai hàm số \(y=x^2\) và \(y=x+2\)
a, vẽ đồ thị của hai hàm số này tren cùng một hệ trục Oxy
b, tìm toạ độ các giao điểm M, N của hai đồ thị trên bằng phép tính
a, bạn tự kẻ hình nha
b,Phương trình hoành độ giao điểm của 2 đồ thị
\(x^2=x+2\) hay \(x^2-x-2=0\)
Phương trình có nghiệm: \(x_1=-1\Rightarrow y_1=1\) và \(x_2=2\Rightarrow y_2=4\)
Vậy 2 đồ thị cắt nhau tại 2 điểm \(M\left(-1;1\right)\) và \(N\left(2;4\right)\)
-Chúc bạn học tốt-
Cho hàm số bậc nhất y=x+2 (d)
a) vẽ đồ thị hàm số trên
b) tìm tọa độ giao điểm của hàm số (d) với đồ thị của hàm số y=2x-1
b: Tọa độ giao điểm là:
2x-1=x+2 và y=x+2
=>3x=3 và y=x+2
=>x=1 và y=3
a: 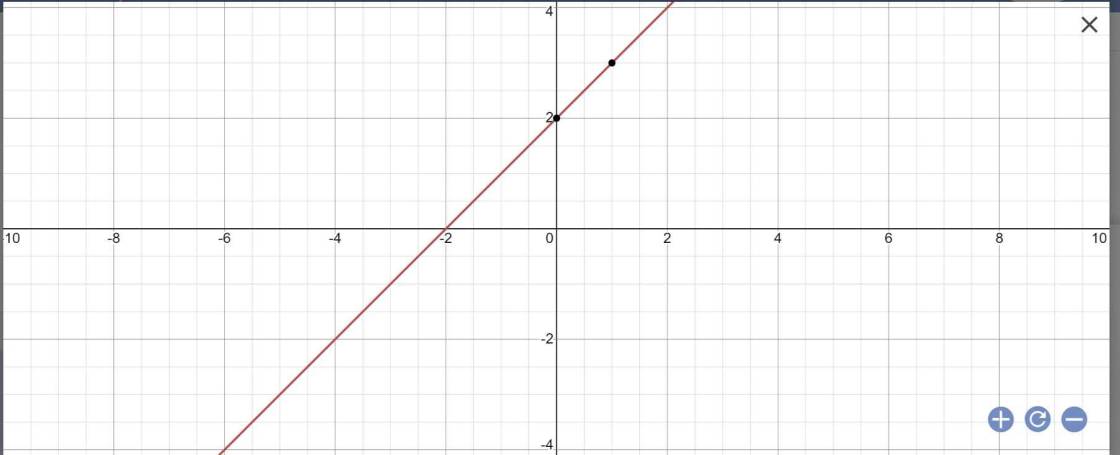
Cho hàm số y=(1-2m)x+3 a) tìm m biết đồ thị hàm số đi qua điểm A(1;0) b) tìm m biết đồ thị hàm số đi qua điểm B(2;-4) c) tìm toạ độ giao điểm của 2 đồ thị hàm số ở câu a,b
a: Thay x=1 và y=0 vào (d), ta được:
1-2m+3=0
\(\Leftrightarrow m=2\)
cho hàm số y=-2x+1a)Xác định tọa độ giao điểm của đồ thị hàm số trên và Ox,Oy
b)CMR:f(x1)+f(x2)=f(x1+x2)+1
c)Tìm tọa độ giao điểm của đồ thị hàm số trên và đồ thị hàm số y=|x|
a) Tọa độ giao điểm của đồ thị hàm số y=-2x+1 với trục Ox là nghiệm của hệ phương trình:
\(\left\{{}\begin{matrix}y=-2x+1\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2x+1=0\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2x=-1\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=0\end{matrix}\right.\)
Tọa độ giao điểm của đồ thị hàm số y=-2x+1 với trục Oy là nghiệm của hệ phương trình:
\(\left\{{}\begin{matrix}x=0\\y=-2x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=-2\cdot0+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\)
Biết đồ thị hàm số bậc bốn y=f(x) được cho bởi hình vẽ bên dưới. Tìm số giao điểm của đồ thị hàm số y=g(x)= [f’(x)]2 – f(x). f’’(x) và trục hoành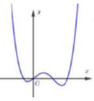
A. 4
B. 0.
C. 6.
D. 2.
Biết rằng đồ thị hàm số bậc 4: y = f(x) được cho như hình vẽ sau:
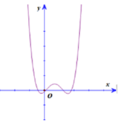
Tìm số giao điểm của đồ thị hàm số y = g(x) = [f’(x)]2 – f(x).f’’(x) và trục Ox
A. 0
B. 2
C. 4
D. 6
Đáp án A
Phương pháp:
Đặt Đáp án A
Phương pháp:
Đặt f(x) = a(x – x1)(x – x2)(x – x3)(x – x4), tính đạo hàm của hàm số y = f(x)
Xét hàm số h x = f ' x f x và chứng minh f(x).f’’(x) – [f’(x)]2 < 0 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
Cách giải: Đồ thị hàm sốy = f(x) cắt trục hoành tại bốn điểm phân biệt nên
f(x) = a(x – x1)(x – x2)(x – x3)(x – x4)
=> f ’(x) = a(x – x1)(x – x2)(x – x3)(x – x4) + a(x – x1)(x – x3)(x – x4) + a(x – x1)(x – x2)(x – x4) + a(x – x1)(x – x2)(x – x3)
f ’(x) = f(x) 1 x - x 1 + 1 x - x 2 + 1 x - x 3 + 1 x - x 4 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4 => f’(x) ≠ 0 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
Đặt h x = f ' x f x = 1 x - x 1 + 1 x - x 2 + 1 x - x 3 + 1 x - x 4 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
Ta có
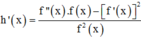
= - 1 ( x - x 1 ) 2 + - 1 ( x - x 2 ) 2 + - 1 ( x - x 3 ) 2 + - 1 ( x - x 4 ) 2 <0 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
=> f ''(x).f(x) – [f’(x)]2 < 0 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
=> g(x) = [f’(x)]2 – f(x).f’’(x)>0 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
Khi f(x) = 0 => f '(x) ≠ 0 => g(x) = [f’(x)]2 – f(x).f’’(x) ≠ 0
Vậy đồ thị hàm số y = g(x) = [f’(x)]2 – f(x).f’’(x) không cắt trục Ox
Cho hai hàm số y = x^2 và y =- x + 2.
a) Vẽ đồ thị của hai hàm số trên cùng một mặt phẳng tọa độ
b) Tìm tọa độ giao điểm của hai đồ thị trên bằng phương pháp đại số
c) Gọi A, B là giao điểm của 2 đồ thị trên. Tính diện tích tam giác AOB
tìm toạ độ giao điểm của đồ thị hàm số y = 4x và đồ thị hàm số y=1/x
Tọa độ giao điểm của đồ thị hàm số \(y=4x\) và y=\(\frac{1}{x}\) là các giá trị x\(\in\) \(Z\) sao cho:
\(4x=\frac{1}{x}\)
\(4x^2=1\)
\(x^2=\frac{1}{4}\)
\(x=\) \(\pm\) \(\sqrt{\frac{1}{2}}\)
\(\implies\) \(\orbr{\begin{cases}x=\frac{1}{2}\\x=-\frac{1}{2}\end{cases}}\) \(\implies\) \(\orbr{\begin{cases}y=4.\frac{1}{2}=2\\y=4.\left(-\frac{1}{2}\right)=-2\end{cases}}\)
\(\implies\) Đồ thị hàm số \(y=4x\) cắt đồ thị hàm số \(y=\frac{1}{x}\) tại \(2\) giao điểm \(\left(\frac{1}{2};2\right),\left(-\frac{1}{2};-2\right)\)
Tọa độ giao điểm của hai đồ thị phải thỏa mãn đồng thời cả hai hàm số
tức là \(\hept{\begin{cases}y=4x\\y=\frac{1}{x}\end{cases}}\)Suy ra \(4x=\frac{1}{x}\Rightarrow4x^2=1\Rightarrow\orbr{\begin{cases}x=\frac{1}{2}\\x=\frac{-1}{2}\end{cases}}\)
Với \(x=\frac{1}{2}\Rightarrow y=\frac{1}{2}.4=2\)
Với \(x=\frac{-1}{2}\Rightarrow y=\frac{-1}{2}.4=-2\)
Vậy hai đồ thị có hai giao điểm là \(M\left(\frac{1}{2};2\right)\)và \(N\left(\frac{-1}{2};-2\right)\)
Chúc các em học tốt!
Cho hàm số y=1/2 x^2 có đồ thị là (P) a) Vẽ đồ thị (P) của hàm số trên b) Tìm toạ độ giao điểm của (P) và đường thẳng (d) : y = x + 4
b: PTHĐGĐ là:
1/2x^2-x-4=0
=>x^2-2x-8=0
=>(x-4)(x+2)=0
=>x=4 hoặc x=-2
=>y=8 hoặc y=2
a: 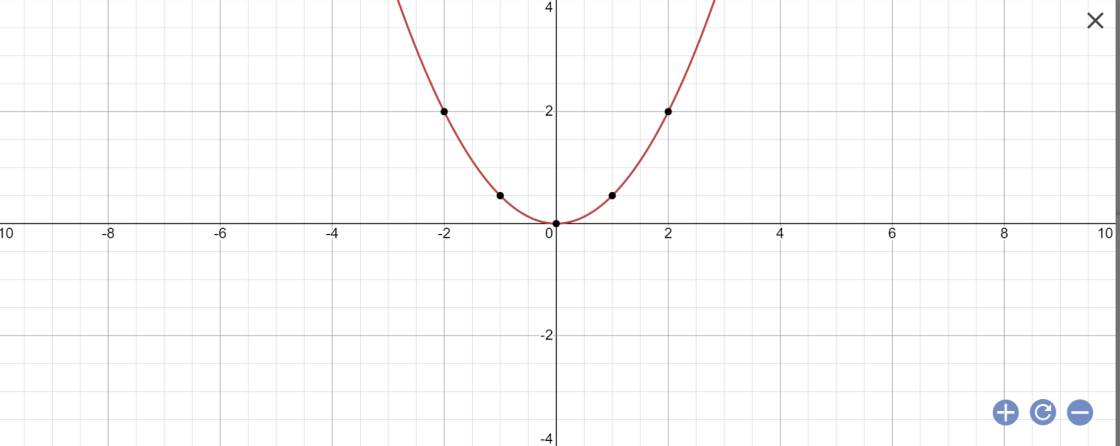
Cho hàm số y = ax2a) Xác định a để đồ thị của hàm số trên đi qua điểm A (4 ; 4).
b) Vẽ đồ thị của hàm số trên với a vừa tìm được và đồ thị của hàm số y = \(-\dfrac{1}{2}x\) trên cùng một mặt phẳng tọa độ Oxy.
c) Tìm tọa độ giao điểm của hai hàm số trên (câu b) bằng phép toán.
a) Để đồ thị hàm số \(y=ax^2\) đi qua điểm A(4;4) thì
Thay x=4 và y=4 vào hàm số \(y=ax^2\), ta được:
\(a\cdot4^2=4\)
\(\Leftrightarrow a\cdot16=4\)
hay \(a=\dfrac{1}{4}\)
a, - Thay tọa độ điểm A vào hàm số ta được : \(4^2.a=4\)
\(\Rightarrow a=\dfrac{1}{4}\)
b, Thay a vào hàm số ta được : \(y=\dfrac{1}{4}x^2\)
- Ta có đồ thì của hai hàm số :
c, - Xét phương trình hoành độ giao điểm :\(\dfrac{1}{4}x^2=-\dfrac{1}{2}x\)
\(\Leftrightarrow x^2+2x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
Vậy hai hàm số trên cắt nhau tại hai điểm : \(\left(0;0\right);\left(-2;1\right)\)