Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng thẳng x = 8 y = - 3 + t là:
A. 1
B. 2
C. 3
D. 4
Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng x = - 1 + 6 t y = - 3 là:
A. ![]() (-1; -3)
(-1; -3)
B.![]() (6; -3)
(6; -3)
C. ![]() (1; -3)
(1; -3)
D.![]() (1; 0)
(1; 0)
Khi phương trình đường thẳng cho dưới dạng tham số: 
Thì đường thẳng có VTCP là ![]() (a; b)
(a; b)
Do đó; phương trình đường thẳng đã cho có vecto chỉ phương là ![]() (6; 0)
(6; 0)
Lại có: vecto ![]() cùng phương với vecto
cùng phương với vecto ![]() nên vecto
nên vecto ![]() cũng là VTCP của đường thẳng đã cho.
cũng là VTCP của đường thẳng đã cho.
Chọn D.
Trong không gian Oxyz, vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng d : x - 1 2 = y - 2 - 1 = z 3
![]()
![]()
![]()
![]()
Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng song song với trục Ox?
![]()
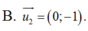
![]()
![]()
Đáp án A
Trục Ox có phương trình tổng quát là: y= 0.
Đường thẳng này có VTPT là ( 0; 1) và VTCP là (1; 0)
Các đường thẳng song song với trục Ox sẽ có cùng VTPT và có cùng VTCP với trục Ox. Nên đường thẳng song song với trục Ox có VTCP là (1; 0) .
Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng song song với trục Ox?
A.(1; 0)
B. (0; 1)
C.(1; 1)
D.Tất cả sai
Đáp án A
Trục Ox có phương trình là y= 0.
Nên đường thẳng này có 1 VTPT là: n → ( 0 ; 1 )
Do đó 1 VTCP của đường thẳng là (1; 0)
Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng song song với trục Oy?
A. (1; 0)
B.(0; -1)
C. (1; 1)
D. (-1; 1)
Đáp án B
Trục Oy có phương trình là x = 0.
Nên đường thẳng này có 1 VTPT là n → ( 1 ; 0 )
Do đó:1 VTCP của đường thẳng là (0; 1)
Mà 2 vectơ (0; 1) và (0; -1) là 2 vectơ cùng phương nên vectơ (0; -1) cũng là VTCP đối với trục Oy.
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x = 1 - t y = 3 z = - 1 + 2 t , vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng d?
A. (-1;3;2)
B. (1;20;-2)
C. (1;3;-1)
D. (1;0;2)
Cho đường thẳng ∆ có một vectơ chỉ phương là u → - 3 ; 5 . Vectơ nào dưới đây không phải là VTCP của ∆?
A, u 1 → 3 ; − 5
B. u 2 → − 6 ; 10
C. u 3 → − 1 ; 5 3
D. u 4 → 5 ; 3
Các vectơ khác vectơ – không, cùng phương (tọa độ tỉ lệ) với u → thì đều là VTCP của đường thẳng ∆.
Ta có: − 3 3 = 5 − 5 ; − 3 − 6 = 5 10 ; − 3 − 1 = 5 5 3 ; − 3 5 ≠ 5 3
Do đó vectơ ở phương án D không phải là VTCP của ∆ .
Trong mặt phẳng Oxy, vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng có phương trình 3 x - 4 y + 5 = 0 .
![]()
![]()
![]()
![]()
Trong mặt phẳng Oxy, vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng có phương trình 3x-4y+5=0.
A. u 2 → =(3;-4).
B. u 1 → =(4;-3).
C. u 3 → =(3;4).
D. u 4 → =(4;3).