Đáp án A
Trục Ox có phương trình là y= 0.
Nên đường thẳng này có 1 VTPT là: n → ( 0 ; 1 )
Do đó 1 VTCP của đường thẳng là (1; 0)
Đáp án A
Trục Ox có phương trình là y= 0.
Nên đường thẳng này có 1 VTPT là: n → ( 0 ; 1 )
Do đó 1 VTCP của đường thẳng là (1; 0)
Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng song song với trục Ox?
![]()
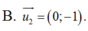
![]()
![]()
Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng song song với trục Oy?
A. (1; 0)
B.(0; -1)
C. (1; 1)
D. (-1; 1)
Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng song song với trục Ox?
A. (0; 1)
B. (1; 0)
C. (-1; 1)
D. (1; 1)
Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng song song với trục Oy?
A. (0; -3)
B. (1; -1)
C. (-3; 0)
D.( 3; 3)
Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua hai điểm A(1; 2) và B(3; 6)?
![]()
![]()
![]()
![]()
Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng x = - 1 + 6 t y = - 3 là:
A. ![]() (-1; -3)
(-1; -3)
B.![]() (6; -3)
(6; -3)
C. ![]() (1; -3)
(1; -3)
D.![]() (1; 0)
(1; 0)
Đường thẳng d có một vectơ chỉ phương là u → = ( 3 ; - 4 ) . Đường thẳng ∆ song song với d có một vectơ pháp tuyến là:
![]()
![]()
![]()
![]()
Đường thẳng d có một vectơ pháp tuyến là n → = ( - 2 ; - 5 ) Đường thẳng ∆ song song với d có một vectơ chỉ phương là:
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho đường thẳng d đi qua điểm M và có vectơ chỉ phương là u → ; cho đường thẳng d’ đi qua điểm M’ và có vectơ chỉ phương là u ' → thỏa mãn [ u → , u ' → ] . MM ' → = 0. Trong những kết luận dưới đây, kết luận nào sai?
A. d và d’ chéo nhau
B. d và d’ có thể song song với nhau
C. d và d’ có thể cắt nhau
D. d và d’ có thể trùng nhau