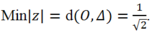Tìm số phức z thỏa mãn (z - 1)(
z
¯
+ 2i) là số thực và |z| đạt giá trị nhỏ nhất. A. z 1+ 2i
Đọc tiếp
Tìm số phức z thỏa mãn (z - 1)( z ¯ + 2i) là số thực và |z| đạt giá trị nhỏ nhất.
A. z = 1+ 2i
Những câu hỏi liên quan
Cho z là số phức thỏa mãn | z ¯ | = |z+2i|. Giá trị nhỏ nhất của |z-1+2i| + |z+1+3i| là
A . 5
B . 5 2
C . 13
D . 29
Cho các số phức z thỏa mãn
z
2
+
4
(
z
-
2
i
)
(
z
-
1
+
2
i
)
. Tìm giá trị nhỏ nhất của
P...
Đọc tiếp
Cho các số phức z thỏa mãn z 2 + 4 = ( z - 2 i ) ( z - 1 + 2 i ) . Tìm giá trị nhỏ nhất của P = z + 3 - 2 i .
Xét các số phức za+bi (a,b thuộc R) thỏa mãn |z-3-2i|2. Tính a+b khi |z+1-2i|+2|z-2-5i| đạt giá trị nhỏ nhất A.
4
-
3
B.
2
+
3
C. 3 D.
4
+
3
Đọc tiếp
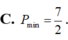
Xét các số phức z=a+bi (a,b thuộc R) thỏa mãn |z-3-2i|=2. Tính a+b khi |z+1-2i|+2|z-2-5i| đạt giá trị nhỏ nhất
A. 4 - 3
B. 2 + 3
C. 3
D. 4 + 3
Xét các số phức za+bi
(
a
,
b
∈
R
)
thỏa mãn
z
-
3
-
2
i
2
. Tính a+b khi
z
+
1
-
2
i
+
2
z
-
2
-
5
i
đạt g...
Đọc tiếp
Xét các số phức z=a+bi ( a , b ∈ R ) thỏa mãn z - 3 - 2 i = 2 . Tính a+b khi z + 1 - 2 i + 2 z - 2 - 5 i đạt giá trị nhỏ nhất.
Xét các số phức
z
a
+
b
i
thỏa mãn
z
-
3
-
2
i
2
. Tính a-b biết biểu thức
S
z
+
1
-
2
i
+
2
z...
Đọc tiếp
Xét các số phức z = a + b i thỏa mãn z - 3 - 2 i = 2 . Tính a-b biết biểu thức S = z + 1 - 2 i + 2 z - 2 - 5 i đạt giá trị nhỏ nhất.
A. - 3
B. 3
C. 4
D. 0
Xét các số phức z a +bi thỏa mãn
z
-
3
-
2
i
2
Tính a-b biết biểu thức
S
z
+
1
-
2
i...
Đọc tiếp
Xét các số phức z = a +bi thỏa mãn z - 3 - 2 i = 2 Tính a-b biết biểu thức S = z + 1 - 2 i + 2 z - 2 - 5 i đạt giá trị nhỏ nhất.
A. - 3
B. 3
C. 4
D. 0
Cho số phức z thỏa mãn
z
+
i
+
1
z
¯
−
2
i
. Tìm giá trị nhỏ nhất của mô đun của số phức z. A.
1
2
B.
2
C.
1...
Đọc tiếp
Cho số phức z thỏa mãn z + i + 1 = z ¯ − 2 i . Tìm giá trị nhỏ nhất của mô đun của số phức z.
A. 1 2
B. 2
C. 1 2
D. 1 4
Cho số phức z thỏa mãn |z+i+1||
z
-2i|. Tìm giá trị nhỏ nhất của mô đun của số phức z. A.
1
2
B.
1
2
C.
2
D.
1
4
Đọc tiếp
Cho số phức z thỏa mãn |z+i+1|=| z -2i|. Tìm giá trị nhỏ nhất của mô đun của số phức z.
A. 1 2
B. 1 2
C. 2
D. 1 4
Cho số phức z thỏa mãn |z +1 +i | =| z ¯ - 2i |. Tìm giá trị nhỏ nhất của |z|.
A. 2
B. 1
C. 1 2
D. 2
Chọn C.
Gọi z = x+ yi thì M (x; y) là điểm biểu diễn z
Ta có 
Nên ( x + 1) 2 + (y + 1) 2 = x2 + (y + 2) 2 hay ∆: x – y – 1 = 0.
Do đó điểm M di chuyển trên ∆. Do đó; để modul của số phức z min khi M là hình chiếu của O trên ∆
Vậy 
Đúng 0
Bình luận (0)