Xét 2 trường hợp:

Th1: 1 điểm trên d1, 2 điểm trên d2

Chọn 1 điểm trên d1 có \(C_{17}^1\) (cách)

Chọn 2 điểm trên d2 có \(C^2_{20}\) (cách)

\(\Rightarrow C^1_{17}.C^2_{20}\) (tam giác)

Th2: 1 điểm trên d2, 2 điểm trên d1

Chọn 1 điểm trên d2 \(C^1_{20}\left(cach\right)\)

Chọn 2 điểm trên d1 \(C^2_{17}\left(cach\right)\)

\(\Rightarrow C^1_{20}.C^2_{17}\left(tam-giac\right)\)

\(\Rightarrow C^1_{17}.C^2_{20}+C^2_{17}.C^1_{20}=...\left(tam-giac\right)\)

( Tớ giải bài 2 thôi nhé! )
Nếu số cần tìm trừ đi 4 thì số mới chia hết cho cả 5 ; 6 và 7.
Mà BCNN { 5 ; 6 ; 7 } = 210     ( do lớn hơn 4 )
Vậy số cần tìm là:    210 + 4 = 214

Đáp số: 214

khó quá à

để (d) song song zới đường thẳng (d') 

=>\(\hept{\begin{cases}m+1=3\\-2m\ne4\end{cases}=>\hept{\begin{cases}m=2\\m\ne-2\end{cases}=>m=2}}\)

b)phương trình hoành độ giao điểm của (d) zà (P)

\(\frac{1}{2}x^2-\left(m+1\right)x+2m=0\Rightarrow x^2-2\left(m+1\right)x+4m=0\)

ta có \(\Delta=4\left(m+1\right)^2-4.4m=4\left(m^2+2m+1\right)-16m=4m^2-8m+4=4\left(m-1\right)^2\ge0\)

để d cắt P tại hai điểm phân biệt 

=>\(\Delta>0=>\left(m-1\right)^2>0=>m\ne1\)(1)

lại có \(\hept{\begin{cases}x_1+x_2=2\left(m+1\right)\\x_1x_2=4m\end{cases}}\)

để 2 hoành độ dương \(\Leftrightarrow\hept{\begin{cases}x_1+x_2>0\\x_1x_2>0\end{cases}=>\hept{\begin{cases}2\left(m+1\right)>0\\4m>0\end{cases}=>\hept{\begin{cases}m>-1\\m>0\end{cases}\Rightarrow m>0}}\left(2\right)}\)

từ 1 zà 2 => m khác 1 , m lớn hơn 0 thì (d) cắt (P) tạ điểm phân biệt có hoành độ dương

a: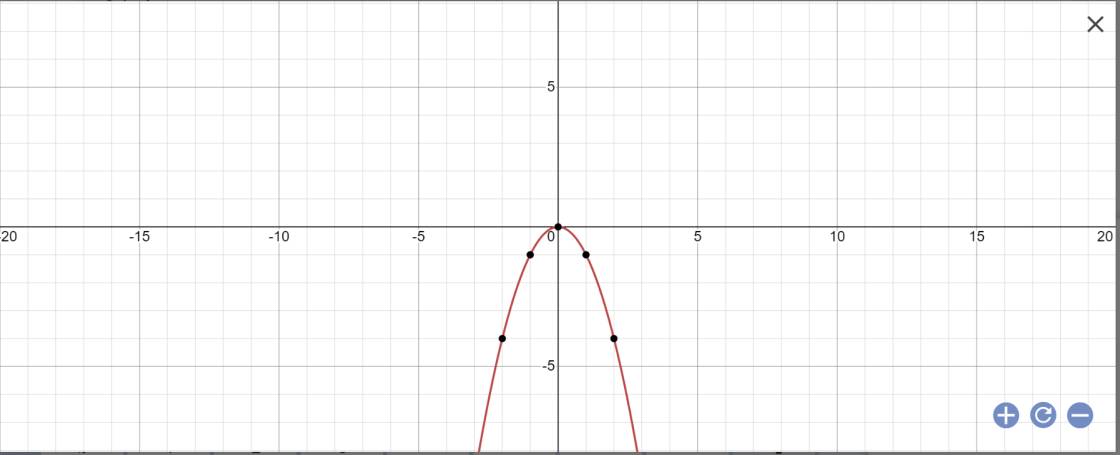 

b: Phương trình OA có dạng là y=ax+b

Theo đề, ta có hệ:

0a+b=0 và a+b=1

=>b=0 và a=1

=>y=x

Vì (d)//OA nên (d): y=x+b

Thay x=2 và y=0 vào (d), ta được:

b+2=0

=>b=-2

=>y=x-2

PTHĐGĐ là:

-x^2-x+2=0

vì a*c<0

nên (P) luôn cắt (d) tại hai điểm phân biệt

Đáp án C

2. Nếu 3 mặt phẳng đôi một cắt nhau theo 3 giao tuyến phân biệt thì 3 giao tuyến ấy hoặc đồng quy, hoặc đôi một song song với nhau

8. Cho 2 đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia

Kẻ OF//BC(F thuộc AC)

=>OF//DE//BC

DE//BC

=>góc DEA=góc ACB

=>góc DEO=1/2*góc ACB

ED//OF
=>góc DEA=góc CFD và góc DEO=góc EOF

=>góc EOF=1/2*góc ACB

=>góc DEO=góc EOF

OF//BC

=>góc FOB=góc OBC=1/2góc ABC

góc BOE=góc BOF+góc EOF

=1/2(góc ABC+góc ACB)