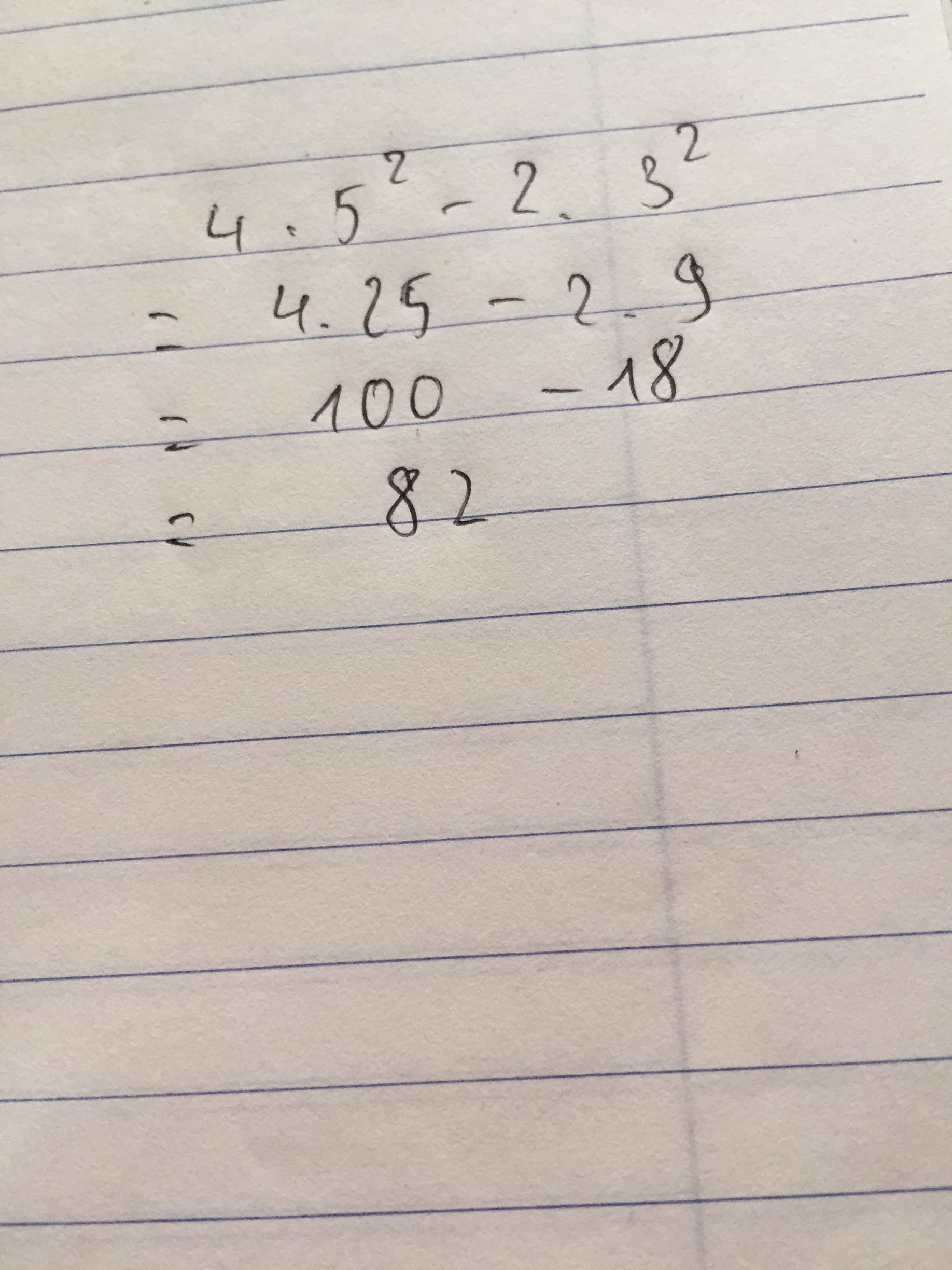tính: 1.22+2.32+3.42+4.52+...+(n-1)n2
Những câu hỏi liên quan
Tính : Q = 1.22 + 2.32 + 3.42 + …+ 19. 202
Q=1.2.(3-1)+2.3.(4-1)+3.4.(5-1)+...+19.20.(21-1)=
=(1.2.3+2.3.4+3.4.5+...+19.20.21)-(1.2+2.3+3.4+...+19.20)
Đặt
A=1.2.3+2.3.4+3.4.5+...+19.20.21
4A=1.2.3.4+2.3.4.4+3.4.5.4+...+19.20.21.4=
=1.2.3.4+2.3.4(5-1)+3.4.5.(6-2)+...+19.20.21.(22-18)=
=1.2.3.4-1.2.3.4+2.3.4.5-2.3.4.5+3.4.5.6-...-18.19.20.21+19.20.21.22=
=19.20.21.22
\(A=\dfrac{19.20.21.22}{4}=5.19.21.22\)
Đặt
B=1.2+2.3+3.4+...+19.20
3B=1.2.3+2.3.3+3.4.3+...+19.20.3=
=1.2.3+2.3.(4-1)+3.4.(5-2)+...+19.20.(21-18)=
=1.2.3-1.2.3+2.3.4-2.3.4+3.4.5-...-18.19.20+19.20.21=
=19.20.21
\(B=\dfrac{19.20.21}{3}=7.19.20\)
Q=A-B
Đúng 1
Bình luận (0)
16 tháng 12 2023 lúc 9:45
A=1.22+2.32+3.42+...+2017.20182
D=1.22+2.32+3.42+...........+99.1002
Các số có tổng từ 1->100 có tổng là:2600
Có 200 số 2 nên ta lấy
2600.200=520 000
=>D=520 000
Đúng 0
Bình luận (0)
3 tháng 1 2021 lúc 19:32
Tính: A = 1.22 + 2.32 + 3.44 + ....+ 2017.20182
Tính giá trị của biểu thức: 4.52 - 2.32
giúp mình với
=2.2.52-2.32
=2.50-2.9
=2.(50-9)
=2.41=82
Đúng 0
Bình luận (0)
Rút gọn phân số sau:
T=1.2.4+2.3.5+3.4.6+...+100.101.103 / 1.12+ 2.32+ 3.42+...+ 100.302
Tính P/Q biết:
P = 1/2.32 + 1/3.33 + ... + 1/n.(n+30) + ... + 1/1973.2003
Q = 1/2.1974 + 1/3.1975 + ... + 1/n.(n+1972) + ... + 1/31.2003
\(P=...\)
\(=\frac{1}{30}\left(\frac{30}{2.32}+\frac{30}{3.33}+...+\frac{30}{1973.2003}\right)\)
\(=\frac{1}{30}\left(\frac{1}{2}-\frac{1}{32}+\frac{1}{3}-\frac{1}{33}+...+\frac{1}{1973}-\frac{1}{2003}\right)\)
\(=\frac{1}{30}\left[\left(\frac{1}{2}+\frac{1}{3}+...+\frac{1}{1973}\right)-\left(\frac{1}{32}+\frac{1}{33}+...+\frac{1}{2003}\right)\right]\)
\(=\frac{1}{30}\left[\left(\frac{1}{2}+\frac{1}{3}+...+\frac{1}{31}\right)-\left(\frac{1}{1974}+\frac{1}{1975}+...+\frac{1}{2003}\right)\right]\)
Đúng 0
Bình luận (0)
\(Q=...\)
\(=\frac{1}{1972}\left(\frac{1972}{2.1974}+\frac{1972}{3.1975}+...+\frac{1}{31.2003}\right)\)
\(=\frac{1}{1972}\left(\frac{1}{2}-\frac{1}{1974}+\frac{1}{3}-\frac{1}{1975}+...+\frac{1}{31}-\frac{1}{2003}\right)\)
\(=\frac{1}{1972}\left[\left(\frac{1}{2}+\frac{1}{3}+...+\frac{1}{31}\right)-\left(\frac{1}{1974}+\frac{1}{1975}+...+\frac{1}{2003}\right)\right]\)
Đúng 0
Bình luận (0)
Gọi \(\left[\left(\frac{1}{2}+\frac{1}{3}+...+\frac{1}{31}\right)-\left(\frac{1}{1974}+\frac{1}{1975}+...+\frac{1}{2003}\right)\right]=A\)
Ta có:\(\frac{P}{Q}=\left(\frac{1}{30}.A\right):\left(\frac{1}{1972}.A\right)=\frac{A}{30}\cdot\frac{1972}{A}=\frac{1972}{30}=\frac{986}{15}\)
Đúng 0
Bình luận (0)
Cho A=1/1.21+1/1.22+1/3.23+...+1/80.100
B=1/1.81+1/2.82+1/3.83+...+1/20.100
Tính A/B
A=20/1.21+20/2.22+...+20/80.100
=1-1/21+1/2-1/22+...+1/80-1/100
=(1+1/2+...+1/80)-(1/21+1/22+...+1/100)
80B=80/1.81+80/2.82+...+8/20.100
=1-1/81+1/2-1/82+...+1/20-1/100
=(1+1/2+...+1/20)-(1/81+1/82+...+1/100)
=(1+1/2+1/3+...+1/20+1/21+1/22+...+1/80)-(1/21+1/22+...1/80+1/81+1/82+...1/100)
=>20A=80B
=>A=4B
Đúng 1
Bình luận (0)
Thực hiện phép tính:a)
(
7
.
5
8
–
8
.
5
4
+
12
5
)
:
5
2
;b)
(
3
.
4
2
+
8
2...
Đọc tiếp
Thực hiện phép tính:
a) ( 7 . 5 8 – 8 . 5 4 + 12 5 ) : 5 2 ;
b) ( 3 . 4 2 + 8 2 + 3 . 16 2 ) : 2 3 .
20 tháng 10 2023 lúc 6:02
Tính:
A= 75 : 73 + 2.32
A = 7⁵ : 7³ + 2.3²
= 7² + 2.9
= 49 + 18
= 67
Đúng 1
Bình luận (0)
\(A=7^5:7^3+2\cdot3^2\)
\(A=7^{5-3}+2\cdot9\)
\(A=7^2+18\)
\(A=49+18\)
\(A=67\)
Đúng 1
Bình luận (2)
A = 75 : 73 + 2 . 32
A = 75 - 3 +2 . 9
A = 49 + 18
A = 67
Đúng 0
Bình luận (0)