Cho tam giác ABC vuông tại A có BC = 12 cm, B ^ = 40 ° . Tính (làm tròn đến chữ số thập phân thứ 2)
A. A C ≈ 7 , 71 ; C ^ = 40 °
B. A C ≈ 7 , 72 ; C ^ = 50 °
C. A C ≈ 7 , 71 ; C ^ = 50 °
D. A C ≈ 7 , 73 ; C ^ = 50 °
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A có BC 12 cm,
B
^
40
°
. Tính (làm tròn đến chữ số thập phân thứ 2) A.
A
C
≈
7
,
71
;
C
^
40
°
B.
A
C
≈
7
,
72
;
C
^
50
°...
Đọc tiếp
Cho tam giác ABC vuông tại A có BC = 12 cm, B ^ = 40 ° . Tính (làm tròn đến chữ số thập phân thứ 2)
A. A C ≈ 7 , 71 ; C ^ = 40 °
B. A C ≈ 7 , 72 ; C ^ = 50 °
C. A C ≈ 7 , 71 ; C ^ = 50 °
D. A C ≈ 7 , 73 ; C ^ = 50 °
Cho tam giác ABC vuông tại A có AB = 12 cm, AC = 16 cm. Vẽ đường cao AH. a) Chứng minh HBA ABC b) Tính BC, AH, BH. c) Vẽ đường phân giác AD của tam giác ABC (D BC). Tính BD, CD. (Làm tròn kết quả đến chữ số thập phân thứ nhất ) d) Trên AH lấy điểm K sao cho AK = 3,6cm. Từ K kẽ đường thẳng song song BC cắt AB và AC lần lượt tại M và N. Tính diện tích tứ giác BMNC
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: BC=căn 12^2+16^2=20cm
AH=12*16/20=9,6cm
BH=AB^2/BC=7,2cm
c: AD là phân giác
=>BD/AB=CD/AC
=>BD/3=CD/4=(BD+CD)/(3+4)=20/7
=>BD=60/7\(\simeq8,6\left(cm\right)\) và CD=80/7\(\simeq11,4\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = 6 cm, AC = 4,5 cm và BC = 7,5 cm. a) Chứng minh tam giác ABC vuông tại A. b) Tính các góc B, C và đường cao AH của tam giác đó (Góc làm tròn đến phút, độ dài làm tròn đến chữ số thập phân thứ nhất)
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}=\dfrac{3}{5}\)
nên \(\widehat{B}\simeq36^052'\)
Ta có: ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{C}=90^0-36^052'=53^08'\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot7,5=4,5\cdot6=27\)
=>AH=27/7,5=3,6(cm)
Đúng 1
Bình luận (0)
: Cho tam giác ABC vuông tại A có AB 12 cm, 500 a) Tính độ dài BC và AC? b) Kẻ tia phân giác BD của góc ABC (D AC). Tính AD, DC, BD? (Kết quả về cạnh làm tròn đến chữ số thập phân thứ hai)
Đọc tiếp
: Cho tam giác ABC vuông tại A có AB = 12 cm, 
= 500
a) Tính độ dài BC và AC?
b) Kẻ tia phân giác BD của góc ABC (D
AC). Tính AD, DC, BD?
(Kết quả về cạnh làm tròn đến chữ số thập phân thứ hai)
Cho tam giác ABC vuông tại A có BC 15cm,
B
^
55
0
. Tính AC;
C
^
(làm tròn đến chữ số thập phân thứ hai) A.
A
C
≈
12
,
29
;
C
^
45
0
B.
A
C
≈...
Đọc tiếp
Cho tam giác ABC vuông tại A có BC = 15cm, B ^ = 55 0 . Tính AC; C ^ (làm tròn đến chữ số thập phân thứ hai)
A. A C ≈ 12 , 29 ; C ^ = 45 0
B. A C ≈ 12 , 29 ; C ^ = 35 0
C. A C ≈ 12 , 2 ; C ^ = 35 0
D. A C ≈ 12 , 92 ; C ^ = 40 0
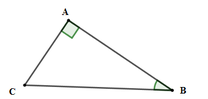
Xét tam giác ABC vuông tại A có:
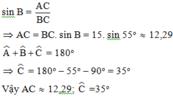
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có BC 12cm,
B
^
40
0
. Tính AC;
C
^
(làm tròn đến chữ số thập phân thứ hai) A.
A
C
≈
7
,
71
;
C
^
40
0
B.
A
C
≈
7...
Đọc tiếp
Cho tam giác ABC vuông tại A có BC = 12cm, B ^ = 40 0 . Tính AC; C ^ (làm tròn đến chữ số thập phân thứ hai)
A. A C ≈ 7 , 71 ; C ^ = 40 0
B. A C ≈ 7 , 72 ; C ^ = 50 0
C. A C ≈ 7 , 71 ; C ^ = 50 0
D. A C ≈ 7 , 73 ; C ^ = 50 0
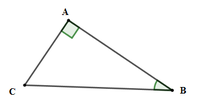
Xét tam giác ABC vuông tại A có:
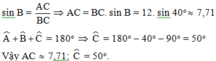
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB = 12 cm, acb = 50 độ 0 a) Tính độ dài BC và AC? b) Kẻ tia phân giác BD của góc ABC (D AC). Tính AD, DC, BD? (Kết quả về cạnh làm tròn đến chữ số thập phân thứ hai)
cho tam giác ABC vuông tại A, B = 60° BC = 20 cm giải tam giác vuông ABC ( làm tròn đến độ đối với số đo góc làm tròn đến chữ số thập phân thứ tư đối với số đo độ dài )
\(AB=\cos B\cdot BC=\dfrac{1}{2}\cdot20=10\left(cm\right)\\ AC=\sin B\cdot BC=\dfrac{\sqrt{3}}{2}\cdot20=10\sqrt{3}\approx17,3205\left(cm\right)\\ \widehat{C}=90^0-\widehat{B}=30^0\)
Đúng 1
Bình luận (1)
Cho tam giác ABC vuông tại A có BC 8cm, AC 6cm. Tính tỉ số lượng giác tanC. (làm tròn đến chữ số thập phân thứ 2) A. tan C
≈
0,87 B. tan C
≈
0,86 C. tan C
≈
0,88 D. tan C
≈
0,89
Đọc tiếp
Cho tam giác ABC vuông tại A có BC = 8cm, AC = 6cm. Tính tỉ số lượng giác tanC. (làm tròn đến chữ số thập phân thứ 2)
A. tan C ≈ 0,87
B. tan C ≈ 0,86
C. tan C ≈ 0,88
D. tan C ≈ 0,89
Theo định lý Py-ta-go ta có:
Xét tam giác ABC vuông tại C có:
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)
