Giả sử khối D1:D4 có các giá trị lần lượt là 4,6,2,-1 thì
=((D1+D3)*D4)/2 có kết quả là:0
tìm tất cả các số nguyên dương n để n=d1^2+d2^2+d3^2+d4^2 trong đó d1,d2,d3,d4 là 4 ước nguyên dương nhỏ nhất của n và d1<d2<d3<d4
Cùng một vật được thả vào bốn bình đựng bốn chất lỏng khác nhau (H.12.4). Hãy dựa vào hình vẽ để so sánh trọng lượng riêng của các chất lỏng.
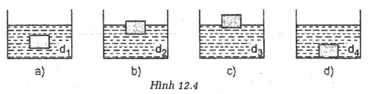
A. d1 > d2 > d3 > d4
B. d4 > d1 > d2 > d3
C. d3 > d2 > d1 > d4
D. d4 > d1 > d3 > d2
Chọn C
Khi vật chìm thì lực đẩy Ác - si – mét FA < P nên d4 < dv. Do đó trọng lượng riêng của chất lỏng d4 là nhỏ nhất. Khi vật lơ lửng trong chất lỏng thì lực đẩy Ác – si – mét FA = P nên dl = dv mà các vật đều giống nhau nên dv là như nhau nên d1 > d4.
Khi vật nổi trên chất lỏng thì lực đẩy Ác – si – mét cân bằng với trọng lượng của vật nên lực đẩy Ác – si – mét trong hai trường hợp đó bằng nhau (bằng trọng lượng của vật).
+ Trường hợp thứ hai: F2 = d2.V2
+ Trường hợp thứ ba: F3 = d3.V3
Mà F2 = F3 và V2 > V3 (V2, V3 là thể tích của phần chất lỏng bị vật chiếm chỗ). Do đó, trọng lượng riêng của chất lỏng thứ hai lớn hơn trọng lượng riêng của chất lỏng thứ nhất hay d2 < d3.
Từ trên ta có: d3 > d2 > d1 > d4
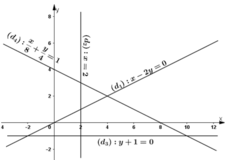
Trong mặt phẳng Oxy, hãy vẽ các đường thẳng có phương trình sau đây:
d1: x – 2y = 0;
d2: x = 2;
d3: y + 1 = 0;
d4: x/8 + y/4 = 1.
+) Đường thẳng d1: x – 2y = 0 đi qua gốc tọa độ O và điểm (2; 1).
+) đường thẳng d2: x = 2 là đường thẳng đi qua điểm (2; 0) và song song với trục Oy.
+) Đường thẳng d3: y +1 = 0 là đường thẳng đi qua điểm (0; -1) và song song với trục Ox.
+) Đường thẳng d4: 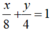 là đường thẳng đi qua điểm (0; 4) và (8; 0).
là đường thẳng đi qua điểm (0; 4) và (8; 0).
Cho hàm số
(d) y=(m2-2)x+m-1
(d1)y=2x-3
(d2)y=-x-2
(d3)y=3x-2
(d4)y=4/5x-1/2
a) (d) // (d1)
b) (d) trùng với (d2)
c)(d) cắt (d3) tại điểm có hoành độ x=-1
d)(d) vuông góc với (d4)
a) Để (d)//(d1) thì \(\left\{{}\begin{matrix}m^2-2=2\\m-1\ne-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2=4\\m\ne-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\in\left\{2;-2\right\}\\m\ne-2\end{matrix}\right.\Leftrightarrow m=2\)
b) Để (d) trùng với (d2) thì
\(\left\{{}\begin{matrix}m^2-2=-1\\m-1=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2=1\\m=-1\end{matrix}\right.\Leftrightarrow m=-1\)
c) Để (d) cắt (d3) thì
\(m^2-2\ne3\)
\(\Leftrightarrow m^2\ne5\)
\(\Leftrightarrow m\notin\left\{\sqrt{5};-\sqrt{5}\right\}\)
Để (d) cắt (d3) tại một điểm có hoành độ x=-1 thì
Thay x=-1 vào hàm số \(y=3x-2\), ta được:
\(y=3\cdot\left(-1\right)-2=-3-2=-5\)
Thay x=-1 và y=-5 vào hàm số \(y=\left(m^2-2\right)x+m-1\), ta được:
\(\left(m^2-2\right)\cdot\left(-1\right)+m-1=-5\)
\(\Leftrightarrow2-m^2+m-1=-5\)
\(\Leftrightarrow-m^2+m-1+5=0\)
\(\Leftrightarrow-m^2+m+4=0\)
\(\Leftrightarrow m^2-m-4=0\)
\(\Leftrightarrow m^2-2\cdot m\cdot\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{17}{4}=0\)
\(\Leftrightarrow\left(m-\dfrac{1}{2}\right)^2=\dfrac{17}{4}\)
\(\Leftrightarrow\left[{}\begin{matrix}m-\dfrac{1}{2}=\dfrac{\sqrt{17}}{2}\\m-\dfrac{1}{2}=-\dfrac{\sqrt{17}}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{\sqrt{17}+1}{2}\left(nhận\right)\\m=\dfrac{1-\sqrt{17}}{2}\left(nhận\right)\end{matrix}\right.\)
d) Để (d) vuông góc với (d4) thì \(\left(m^2-2\right)\cdot\dfrac{4}{5}=-1\)
\(\Leftrightarrow m^2-2=-1:\dfrac{4}{5}=-1\cdot\dfrac{5}{4}=\dfrac{-5}{4}\)
\(\Leftrightarrow m^2=-\dfrac{5}{4}+2=\dfrac{-5}{4}+\dfrac{8}{4}=\dfrac{3}{4}\)
hay \(m\in\left\{\dfrac{\sqrt{3}}{2};-\dfrac{\sqrt{3}}{2}\right\}\)
Cho 4 đt sau : d1 y=x, d2: y= -x+2,d3:y=x-2,d4:y=mx+n . Tìm d4 để đưoengf thẳng d1,d2,d3,d4 cắt nhau tại 4 điểm tạo thành hình vuông
Bài 1: Giả sử cần tính tổng giá trị trong các ô C2 và D4, sau đó nhân với giá trị trong ô B2. Hãy viết công thức hoặc hàm để tính?
Bài 2: Giả sử trong các ô A1, B1 lần lượt chứa các số -4, 3. Em hãy cho biết kết quả của các công thức tính sau:
a. =SUM(A1, B1)
b. =SUM(A1,B1, -5)
c. =AVERAGE(A1, B1, 4)
d. =SUM(A1, B1, B1)
e. =AVERAGE(A1, B1, 5, 0)
Bài 3: Viết công thức tính giá trị của các biểu thức sau:
a. 3 × (15 − 3 2 ) + 6
b. (2+7) 2 7
c. (144 6 − 3) × 5
d. ( 1 2 − 2 3 ) + ( 3 4 − 4 5 )
a) vẽ các đồ thị hàm số sau trên cùng một mặt phẳng tọa độ Oxy
y=\(\dfrac{x+3}{2}\)(d1);y=-2x(d2);y=\(\dfrac{x}{2}-2\)(d3);y=-2x+4(d4)
b)gọi tọa độ các điểm (d1) với (d2) và (d4) theo thứ tự A,B các giao điểm của (d3) với (d2) và (d4) theo thứ tự D,C
+ ABCD là hình gì ?
+ tìm tọa độ giao điểm A,B,C,D và tính diện tích hình đó
a: 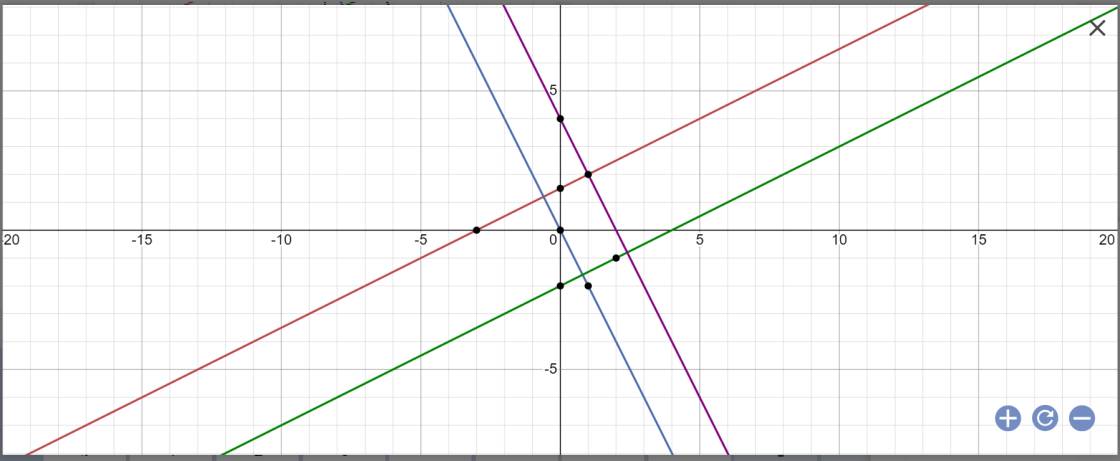
b: (d1): y=1/2x+3/2; (d2): y=-2x; (d3): y=1/2x-2; (d4): y=-2x+4
=>(d1) vuông góc (d2), (d1) vuông góc (d4); (d2) vuông góc (d3); (d2)//(d4)
=>ABCD là hình chữ nhật
=>A(-3/5;6/5); B(2/5;16/5); C(4/5;-8/5); D(12/5;-4/5)
Cho (d1) y = (m +2)x + 3
(d2) y = 3x - 1
(d3) y = 2x + 4
(d4) y = 2mx - 2
a) tìm m để 3 đường thẳng d1, d2 và d3 đồng quy
b) tìm m để d4, d1, d3 đồng quy
<giải tắt>
a/ \(d_2\text{ giao }d_3\text{ tại }A\left(5;14\right)\)
Để d1; d2; d3 đồng quy thì \(A\in d_1\Leftrightarrow14=\left(m+2\right).5+3\Leftrightarrow m=\frac{1}{5}\)
b/ Gọi tọa độ điểm đồng quy là \(M\left(a;2a+4\right)\)(do M thuộc d3)
\(M\in d_1\Rightarrow2a+4=\left(m+2\right)a+3\Leftrightarrow ma=1\)
\(M\in d_4\Rightarrow2a+4=2m.a-2\Rightarrow2a+4=2.1-2\Rightarrow a=-2\)
\(\Rightarrow m=\frac{1}{a}=-\frac{1}{2}\)
\(a)\)Pt hoành độ giao điểm của \(d_2\)và \(d_3\)thỏa mãn:
\(3x-1=2x+4\)
\(\Leftrightarrow3x-2x=4+1\)
\(\Leftrightarrow x=5\)
Thay \(x=5\)vào \(y=3x-1\)
\(\Leftrightarrow y=3.5-1=14\)
Vậy \(d_2\)giao \(d_3\)tại \(M\left(5;14\right)\)
\(\Rightarrow d_1\) \(,\)\(d_2\)\(,\)\(d_3\)đồng quy
\(\Leftrightarrow d_1\)cắt \(M\left(5;14\right)\)
\(\Leftrightarrow\left(m+2\right).5+3=14\)
\(\Leftrightarrow m+2=\frac{11}{5}\)
\(\Leftrightarrow m=\frac{1}{5}\)
Với giá trị các ô D1=20, D2=30, D3=10. Hãy cho biết kết quả của công thức =Min (D1: D3, 40) là giá trị nào sau đây?