Cho x, y là các số thực tùy ý. Mệnh đề nào sau đây là đúng
A. e x + y = e x + e y
B. e x - y = e x - e y
C. e x y = e x . e y
D. e x e y = e x - y
Cho x,y,z là các số thực dương tùy ý khác 1 và xyz khác 1. Đặt a = log x , b = log z y . Mệnh đề nào sau đây là đúng?
A . log xyz ( y 3 z 2 ) = 3 ab + 2 a a + b + 1 .
B . log xyz ( y 3 z 2 ) = 3 ab + 2 ab a + b + 1 .
C . log xyz ( y 3 z 2 ) = 3 ab + 2 a ab + a + b .
D . log xyz ( y 3 z 2 ) = 3 ab + 2 b ab + a + b .
Cho x; y; z là các số thực dương tùy ý khác 1 và xyz khác 1. Đặt a = logxy; b = logzy. Mệnh đề nào sau đây đúng?
A. log x y z y 3 z 2 = 3 a b + 2 a a + b + 1
B. log x y z y 3 z 2 = 3 a b + 2 b a b + a + b
C. log x y z y 3 z 2 = 3 a b + 2 a a b + a + b
D. log x y z y 3 z 2 = 3 a b + 2 b a + b + 1
Chọn C.
Ta có: logxyz( y3z2) = 3logxyzy + 2logxyzz
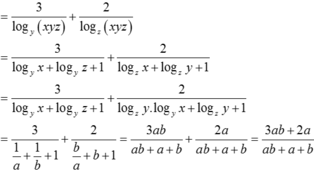
Với các số thực dương x,y tùy ý , đặt log 3 x = a , log 3 y = b . Mệnh đề nào dưới đây là đúng ?
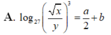
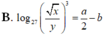
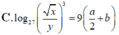
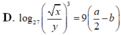
Cho hai hàm số y=f(x), y=g(x) liên tục trên R với k là số thực tùy ý. Mệnh đề nào dưới đây sai?
A. ∫ f x + g x d x = ∫ f ( x ) d x + ∫ g ( x ) d x
B. ∫ k . f ( x ) d x = k . ∫ f ( x ) d x
C. ∫ f x - g x d x = ∫ f ( x ) d x - ∫ g ( x ) d x
D. f ( x ) d x ' = f ( x )
Chú ý ∫ k . f ( x ) d x = k . ∫ f ( x ) d x chỉ đúng với k # 0 , k ∈ ℝ
Chọn đáp án B.
Cho hai số thực a, b tùy ý, F(x) là một nguyên hàm của hàm số f(x) trên tập ℝ . Mệnh đề nào dưới đây là đúng?
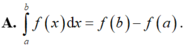
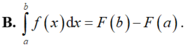
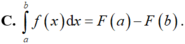
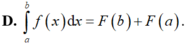
Với x là số thực dương tùy ý, mệnh đề nào dưới đây đúng?
A. log 100 x = log x
B. log 100 x = 2 log x
C. log 100 x = 1 2 log x
D. log 100 x = - log x
Cho a là số thực dương tùy ý. Mệnh đề nào sau đây đúng?
A. log 3 9 a = 2 - log 3 a
B. log 3 9 a = 2 log 3 a
C. log 3 9 a = 2 + log 3 a
D. log 3 9 a = 9 log 3 a
Cho a là số thực dương tùy ý. Mệnh đề nào sau đây đúng?
A. log 3 3 a 2 = 3 − 2 log 3 a
B. log 3 3 a 2 = 1 + 2 log 3 a
C. log 3 3 a 2 = 3 − 1 2 log 3 a
D. log 3 3 a 2 = 1 − 2 log 3 a
Cho a là số thực dương tùy ý. Mệnh đề nào sau đây đúng?
A. l o g 3 3 a 2 = 3 − 1 2 log 3 a .
B. log 3 3 a 2 = 3 − 2 log 3 a .
C. l o g 3 3 a 2 = 1 − 2 log 3 a .
D. l o g 3 3 a 2 = 1 + 2 log 3 a .
Đáp án C.
Phương pháp:
Sử dụng các công thức của logarit:
log a b c = log a b − log a c , a , b , c > 0 , a ≠ 1
log a b c = c log a b , a , b > 0 , a ≠ 1
Cách giải:
log 3 3 a 2 = log 3 3 − log 3 a 2 = 1 − 2 log 3 a .