Biết rằng đồ thị hàm y = ( m - 2 n - 3 ) x + 5 x - m - n số nhận hai trục tọa độ làm hai đường tiệm cận. Tính tổng S = m 2 + n 2 - 2 .
A.S=2
B.S=0
C.S=-1
D.S=1
Những câu hỏi liên quan
5 tháng 9 2023 lúc 21:09
Cho hàm số \(y=mx+m-6\left(m\ne0\right)\left(1\right)\).
1) Xác định m biết đồ thị hàm số (1) đi qua điểm M(2; 3). Vẽ đồ thị hàm số (1) với m vừa tìm được.
2) Tìm m để đồ thị hàm số (1) song song với đường thẳng \(y=3x+2\)
3) Chứng minh rằng đồ thị hàm số (1) luôn đi qua một điểm cố định với mọi giá trị của tham số m
1. Đồ thị của hàm số đi qua điểm \(M\left(2;3\right)\) nên giá trị hoành độ và tung độ của \(M\) là nghiệm của phương trình đường thẳng trên, tức:
\(3=m\cdot2+m-6\Leftrightarrow m=3\left(TM\right)\)
2. Đồ thị hàm số song song với đường thẳng \(\left(d\right):y=3x+2\), khi: \(\left\{{}\begin{matrix}m=3\\m-6\ne2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=3\\m\ne8\end{matrix}\right.\Rightarrow m=3\left(TM\right)\)
3. Gọi \(P\left(x_0;y_0\right)\) là điểm cố định mà đồ thị hàm số đi qua với mọi giá trị \(m\).
Khi đó: \(mx_0+m-6=y_0\Leftrightarrow\left(x_0+1\right)m-\left(y_0+6\right)=0\left(I\right)\)
Suy ra, phương trình \(\left(I\right)\) có vô số nghiệm, điều này xảy ra khi: \(\left\{{}\begin{matrix}x_0+1=0\\y_0+6=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=-1\\y_0=-6\end{matrix}\right.\).
Vậy: Điểm cố định mà đồ thị hàm số luôn đi qua với mọi giá trị \(m\) là \(P\left(-1;-6\right)\).
Đúng 4
Bình luận (0)
Cho đồ thị hàm số y = (m -2)x + 8. Tìm m biết rằng đồ thị hàm số cắt trục hoành tại tại điểm có hoành độ là 2?
A. m = -2
B. m = 2
C. m = 1
D. m = -1
Đáp án A
Vì đồ thị hàm số cắt trục hoành tại tại điểm có hoành độ là 2 nên điểm A(2; 0) thuộc đồ thị hàm số đã cho.
Thay x = 2; y = 0 ta được: 0 = (m -2).2 + 8
⇔ 0 = 2m - 4 + 8 ⇔ 0 = 2m + 4 ⇔ m = -2
Đúng 0
Bình luận (0)
Câu 1: Cho hàm số y = - 2x + 2 có đồ thị là (d) a) Vẽ đồ thị (d) của hàm số trên b) Tìm trên d hat o thi (d) điểm P có hoành độ bằng – 2 c) Xác định giá trị m của hàm số y = mx + m + m ^ 2 biết rằng hàm số này đồng biến và đồ thị của nó cắt đồ thị (d) nói trên tại điểm Q có hoành độ là x = - 1
Tìm m biết rằng điêm A(m-14) thuộc đồ thị hàm số y=-3,5x
Tìm p biết rằng điểm B(-0,35b) thuộc đồ thị hàm số y=1/7x
Bài 1.Xác định m, biết rằng đồ thị hàm số y=(m-1) x đi qua điểm A (2;-6).Hãy vẽ đồ thị của hàm số trên với m vừa tìm được.
\(A\left(2;-6\right)\inđths\Leftrightarrow2m-2=-6\Leftrightarrow m=-2\)
Đúng 4
Bình luận (1)
Cho hàm số y = ax. Tìm a biết rằng M (1;-2) thuộc đồ thị hàm số.
A. a = 2
B. a = -2
C. a = 1
D. a = 3
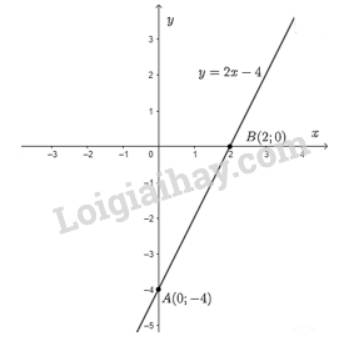
Cho hàm số bậc nhất \(y = ax - 4\)
a) Tìm hệ số góc \(a\) biết rằng đồ thị hàm số đi qua điểm \(M\left( {1; - 2} \right)\).
b) Vẽ đồ thị của hàm số.
a) Vì đồ thị hàm số đi qua điểm \(M\left( {1; - 2} \right)\)nên ta có:
\( - 2 = a.1 - 4 \Leftrightarrow a = - 2 + 4 = 2\)
Hàm số cần tìm là \(y = 2x - 4\) có hệ số góc \(a = 2\).
b) Cho \(x = 0 \Rightarrow y = - 4\) ta được điểm \(A\left( {0; - 4} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{4}{2} = 2\) ta được điểm \(B\left( {2;0} \right)\) trên \(Ox\).
Đồ thị hàm số là đường thẳng đi qua hai điểm \(A\) và \(B\).
Đúng 0
Bình luận (0)
Cho hàm số y = -2x + 2 có đồ thị là (d)
a)Vẽ đồ thị của hàm số trên
b) Tìm trên đồ thị (d) điểm P có hoành độ bằng -2
c) Xác định giá trị m của hàm số y = mx + m+m2 biết rằng hàm số này đồng biến và đồ thị của nó cắt đồ thị (d) nói trên tại điểm Q có hoành độ x = -1
Biết rằng đồ thị hàm số y = f(x) = 2x + 5 và đồ thị hàm số y = f(x) = x + 3 cắt nhau tại điểm M. Không vẽ đồ thị, hãy tìm tọa độ của điểm M.
M thuộc đồ thị hs y = 2x + 5 => yM = 2xM + 5
M thuộc đths y = x + 3 => yM = xM+ 3
=> 2xM + 5 = xM + 3 => 2xM - xM = 3 -5 => xM = -2
=> yM = xM + 3 = -2 + 3 = 1
Vậy M(1;-2)
Đúng 1
Bình luận (0)
a) Biết rằng điểm M(a;-2,5) thuộc đồ thị hàm số y=-2,5x2. Tìm a?
b) Biết rằng điểm P(3;b) thuộc đồ thị hàm số y=|x-4|. Tìm b?
giúp mk nha m.n mk se tick cho