Đặt \(t=tan\dfrac{x}{2}\Rightarrow\left\{{}\begin{matrix}t\in\left[0;1\right]\\sinx=\dfrac{2t}{1+t^2}\\cosx=\dfrac{1-t^2}{1+t^2}\end{matrix}\right.\)

Pt trở thành: \(\dfrac{m.2t}{1+t^2}+\dfrac{1-t^2}{1+t^2}=1\)

\(\Leftrightarrow2mt+1-t^2=1+t^2\)

\(\Leftrightarrow2mt-2t^2=0\)

\(\Leftrightarrow\left[{}\begin{matrix}t=0\\t=m\end{matrix}\right.\)

\(\Rightarrow\) Để pt có 2 nghiệm thuộc đoạn đã cho thì \(0< m\le1\)

Ta có:  x 2 - 4 x + 6 + 3 m = 0 ⇔ 3 m = - x 2 + 4 x - 6

Số nghiệm của phương trình  x 2 - 4 x + 6 + 3 m = 0 là số giao điểm của đường thẳng  y = 3 m  và parabol  y = - x 2 + 4 x - 6

Parabol  y = - x 2 + 4 x - 6  có hoành độ đỉnh  x = 2 ∈ - 1 ; 3 , hệ số  a = - 1 < 0  nên đồng biến khi  x < 2  và nghịch biến khi  x > 2 .

Bảng biến thiên của hàm số  y = - x 2 + 4 x - 6  trên đoạn  - 1 ; 3 :

Từ bảng biến thiên ta thấy, nếu phương trình có nghiệm trên đoạn  - 1 ; 3  thì đường thẳng  y = 3 m  phải cắt parabol tại ít nhất 1 điểm có hoành độ thuộc đoạn  - 1 ; 3 .

Phương trình có nghiệm thuộc đoạn  - 1 ; 3 ⇔ - 11 ≤ 3 m ≤ - 2 ⇔ − 11 3 ≤ m ≤ − 2 3

Đáp án cần chọn là: B

Đáp án A

Điều kiện: x > 0 .

4 log 4 2 x − 2 log 2 x + 3 − m = 0 ⇔ 4. 1 4 . log 2 2 x − 2 log 2 x + 3 − m = 0 ⇔ log 2 2 x − 2 log 2 x + 3 − m = 0 1 .

Đặt t = log 2 x ta có (1) tương đương

t 2 − 2 t + 3 − m = 0 ⇔ t 2 − 2 t + 3 = m .

Ta tìm giá trị của m để t 2 − 2 t + 3 − m = 0  có nghiệm thuộc đoạn  1 ; 2 .

Khảo sát hàm  y t = t 2 − 2 t + 3.

Ta có  y ' t = 2 t − 2 = 0 ⇔ t = 1.

Bảng biến thiên

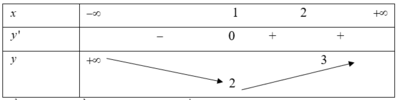
Để thỏa mãn đề bài thì 2 ≤ m ≤ 3 .

Đáp án D

Điều kiện: x > 0.

Đặt t = log 2 x . Khi đó

4 log 2 4 x − 2 log 2 x + 3 − m = 0 ⇔ 4. 1 4 log 2 2 x − 2 log 2 x + 3 − m = 0 ⇔ t 2 − 2 t + 3 − m = 0.

Để thỏa mãn đề bài thì phương trình t 2 − 2 t + 3 − m = 0  có nghiệm thuộc đoạn  − 1 ; 2

t 2 − 2 t + 3 − m = 0 ⇔ t 2 − 2 t + 3 = m .

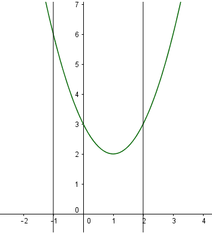
Từ đồ thị hàm số y = t 2 − 2 t + 3  nhân thấy 2 ≤ m ≤ 6  thỏa mãn điều kiện đề bài.