Phương trình s i n x - m = 0 vô nghiệm khi m là:
A. - 1 ≤ m ≤ 1
B. [ m < - 1 m > 1
C. m < -1
D. m > 1
cho phương trình ( m^2-m)x +m^2 -1=0 (m là tham số) a) giải pt khi m=2 b) tìm m để pt có nghiệm x=-1 c) tìm m để pt có nghiệm , vô nghiệm, vô số nghiệm
a.
Khi \(m=2\) pt trở thành:
\(2x+3=0\Rightarrow x=-\dfrac{3}{2}\)
b.
Để pt có nghiệm \(x=-1\)
\(\Rightarrow\left(m^2-m\right).\left(-1\right)+m^2-1=0\)
\(\Leftrightarrow-m^2+m+m^2-1=0\)
\(\Leftrightarrow m-1=0\)
\(\Leftrightarrow m=1\)
c.
Pt tương đương:
\(\left(m^2-m\right)x=-\left(m^2-1\right)\)
\(\Leftrightarrow m\left(m-1\right)x=-\left(m-1\right)\left(m+1\right)\)
Pt vô nghiệm khi:
\(\left\{{}\begin{matrix}m\left(m-1\right)=0\\-\left(m-1\right)\left(m+1\right)\ne0\end{matrix}\right.\) \(\Leftrightarrow m=0\)
\(\Rightarrow\) pt có nghiệm khi \(m\ne0\)
Pt có vô số nghiệm khi:
\(\left\{{}\begin{matrix}m\left(m-1\right)=0\\-\left(m-1\right)\left(m+1\right)=0\end{matrix}\right.\) \(\Leftrightarrow m=1\)
Lời giải:
a. Khi $m=2$ thì pt trở thành:
$2x+3=0\Leftrightarrow x=-\frac{3}{2}$
b. Để pt có nghiệm $x=-1$ thì:
$(m^2-m).(-1)+m^2-1=0$
$\Leftrightarrow m-1=0\Leftrightarrow m=1$
c.
PT $\Leftrightarrow (m^2-m)x=1-m^2$
Để pt vô nghiệm thì: \(\left\{\begin{matrix} m^2-m=0\\ 1-m^2\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m(m-1)=0\\ (1-m)(1+m)\neq 0\end{matrix}\right.\)
\(\Leftrightarrow m=0\)
PT có vô số nghiệm khi \(\left\{\begin{matrix} m^2-m=0\\ 1-m^2= 0\end{matrix}\right.\Leftrightarrow m=1\)
Để PT có nghiệm thì: $m\neq 0$
a Tìm m để phương trình vô nghiệm: x2 - (2m - 3)x + m2 = 0.
b Tìm m để phương trình vô nghiệm: (m - 1)x2 - 2mx + m -2 = 0.
c Tìm m để phương trình vô nghiệm: (2 - m)x2 - 2(m + 1)x + 4 - m = 0
\(a,x^2-\left(2m-3\right)x+m^2=0-vô-ngo\)
\(\Leftrightarrow\Delta< 0\Leftrightarrow[-\left(2m-3\right)]^2-4m^2< 0\Leftrightarrow m>\dfrac{3}{4}\)
\(b,\left(m-1\right)x^2-2mx+m-2=0\)
\(m-1=0\Leftrightarrow m=1\Rightarrow-2x-1=0\Leftrightarrow x=-0,5\left(ktm\right)\)
\(m-1\ne0\Leftrightarrow m\ne1\Rightarrow\Delta'< 0\Leftrightarrow\left(-m\right)^2-\left(m-2\right)\left(m-1\right)< 0\Leftrightarrow m< \dfrac{2}{3}\)
\(c,\left(2-m\right)x^2-2\left(m+1\right)x+4-m=0\)
\(2-m=0\Leftrightarrow m=2\Rightarrow-6x+2=0\Leftrightarrow x=\dfrac{1}{3}\left(ktm\right)\)
\(2-m\ne0\Leftrightarrow m\ne2\Rightarrow\Delta'< 0\Leftrightarrow[-\left(m+1\right)]^2-\left(4-m\right)\left(2-m\right)< 0\Leftrightarrow m< \dfrac{7}{8}\)
Cho phương trình: (m^2-7m+6)x+m^2-1=0 (với m là tham số)
a)tìm m để phương trình có nghiệm duy nhất.
b)tìm m để phương trình có vô số nghiệm.
c)tìm m để phương trình vô nghiệm.
Cho phương trình m(x-4)-2x=4(1-m) (với m là tham số)
a) Giải phương trình với m=0, m=-1, m=-3
b)Tìm m để phương trình vô nghiệm
c)Tìm m để phương trình có vô số nghiệm
d)Tìm m để phương trình có nghiệm dương duy nhất
e)Tìm m để phương trình có nghiệm duy nhât nhỏ hơn 1
Tìm m để phương trình vô nghiệm (m +1)x2 -2 (m + 1)x +m = 0 vô nghiệm?
A. m > -1 B. m ≥ -1 C. m ≤ -1 D. m < 1
Cho phương trình: \(x^2+2x+\left|x+1\right|-m=0\)
giải phương trình khi m=1. Tìm m để phương trình vô nghiệm
Lời giải:
PT $\Leftrightarrow (x+1)^2+|x+1|-(m+1)=0$
$\Leftrightarrow |x+1|^2+|x+1|-(m+1)=0$
Đặt $|x+1|=t(t\geq 0)$ thì: $t^2+t-(m+1)=0(*)$
Với $m=1$ thì $t^2+t-2=0$
$\Leftrightarrow (t-1)(t+2)=0$
Vì $t\geq 0$ nên $t=1\Leftrightarrow |x+1|=1$
$\Leftrightarrow x+1=\pm 1\Leftrightarrow x=0$ hoặc $x=-2$
Để pt vô nghiệm thì $(*)$ chỉ có nghiệm âm hoặc vô nghiệm.
PT $(*)$ chỉ có nghiệm âm khi \(\left\{\begin{matrix} \Delta (*)=1+4(m+1)\geq 0\\ S=-1< 0\\ P=-(m+1)<0\end{matrix}\right.\Leftrightarrow m>-1\)
Để $(*)$ vô nghiệm khi $\Delta=4m+5< 0$
$\Leftrightarrow m< \frac{-5}{4}$
Vậy $m>-1$ hoặc $m< \frac{-5}{4}$
bài tập: cho hệ phương trình \(\left\{{}\begin{matrix}x+my=1\\\\mx+y=1\end{matrix}\right.\) (m là tham số )
a, Giaỉ hệ phương trình khi m=1,m=-1,m=2
b,Tìm m để hệ phương trình đã cho
b.1, có nghiệm duy nhất
b.2,vô nghiệm
b.3,có vô số nghiệm
c,Tìm m để hệ có nghiệm duy nhất \(x+2y=3\)
thankyou
Lời giải:
a) Khi $m=1$ thì HPT trở thành:
\(\left\{\begin{matrix} x+y=1\\ x+y=1\end{matrix}\right.\Leftrightarrow x+y=1\Leftrightarrow y=1-x\)
Khi đó, hệ có nghiệm $(x,y)=(a,1-a)$ với $a$ là số thực bất kỳ.
Khi $m=-1$ thì hệ trở thành:
\(\left\{\begin{matrix} x-y=1\\ -x+y=1\end{matrix}\right.\Rightarrow (x-y)+(-x+y)=2\Leftrightarrow 0=2\) (vô lý)
Vậy HPT vô nghiệm
Khi $m=2$ thì hệ trở thành: \(\left\{\begin{matrix} x+2y=1\\ 2x+y=1\end{matrix}\right.\Rightarrow (x+2y)-(2x+y)=1-1=0\Leftrightarrow y-x=0\Leftrightarrow x=y\)
Thay $x=y$ vào 1 trong 2 PT của hệ thì có: $3x=3y=1\Rightarrow x=y=\frac{1}{3}$Vậy........
b)
PT $(1)\Rightarrow x=1-my$. Thay vào PT $(2)$ có:
$m(1-my)+y=1\Leftrightarrow y(1-m^2)=1-m(*)$
b.1
Để HPT có nghiệm duy nhất thì $(*)$ có nghiệm $y$ duy nhất
Điều này xảy ra khi $1-m^2\neq 0\Leftrightarrow (1-m)(1+m)\neq 0$
$\Leftrightarrow m\neq \pm 1$
b.2 Để HPT vô nghiệm thì $(*)$ vô nghiệm $y$. Điều này xảy ra khi $1-m^2=0$ và $1-m\neq 0$
$\Leftrightarrow m=-1$
b.3 Để HPT vô số nghiệm thì $(*)$ vô số nghiệm $y$. Điều này xảy ra khi $1-m^2=0$ và $1-m=0$
$\Leftrightarrow m=1$
c) Ở b.1 ta có với $m\neq \pm 1$ thì $(*)$ có nghiệm duy nhất $y=\frac{1}{m+1}$
$x=1-my=\frac{1}{m+1}$
Thay vào $x+2y=3$ thì:
$\frac{3}{m+1}=3\Leftrightarrow m=0$
Cho hệ bất phương trình mx + 2 m > 0 2 x + 3 5 > 1 - 3 x 5
Xét các mệnh đề sau:
(I) Khi m< 0 thì hệ bất phương trình đã cho vô nghiệm.
(II) Khi m= 0 thì hệ bất phương trình đã cho có tập nghiệm là R
(III) Khi m≥ 0 thì hệ bất phương trình đã cho có tập nghiệm là 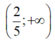
(IV) Khi m> 0 thì hệ bất phương trình đã cho có tập nghiệm là 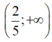
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng ?
A. 1
B. 0
C. 2
D. 3
cho phương trình:
mx - 3 = 2x =2m
1) tìm m để phương trình vô nghiệm, phương trình có nghiệm
2) khi phương trình có nghiệm duy nhất :
a) tìm m nguyên để phương trình có nghiệm nguyên
b) tìm m để phương trình có nghiệm x>0
c) tìm m để phương trình có nghiệm x<0
Cho phương trình :
\(\left(m^2+5m+4\right)x^2=m+4\)
trong đó m là một số. Chứng minh rằng :
a) Khi \(m=-4\), phương trình nghiệm đúng với mọi giá trị của ẩn
b) Khi \(m=-1\), phương trình vô nghiệm
c) Khi \(m=-2\) hoặc \(m=-3\), phương trình cũng vô nghiệm
d) Khi \(m=0\), phương trình nhận \(x=1;x=-1\) là nghiệm
a) Khi \(m=-4\) phương trình trở thành:
\(\left[\left(-4\right)^2+5.\left(-4\right)+4\right]x^2=-4+4\)
\(\Leftrightarrow0.x^2=0\)
Đúng với mọi x.
b) Khi \(m=-1\) phương trình trở thành:
\(\left[\left(-1\right)^2+5.\left(-1\right)+4\right]x^2=-1+4\)
\(\Leftrightarrow0.x^2=3\)
Phương trình vô nghiệm.
c) Khi \(m=-2\) phương trình trở thành:
\(\left[\left(-2\right)^2+5.\left(-2\right)+4\right]x^2=-2+4\)
\(\Leftrightarrow-2.x^2=2\)
\(\Leftrightarrow x^2=-1\)
Phương trình này cũng vô nghiệm.
Khi \(m=-3\) phương trình trở thành:
\(\left[\left(-3\right)^2+5.\left(-3\right)+4\right]x^2=-3+4\)
\(\Leftrightarrow-2x^2=1\)
\(\Leftrightarrow x^2=-\dfrac{1}{2}\)
Phương trình cũng vô nghiệm.
d) Khi \(m=0\) phương trình trở thành:
\(\left[0^2+5.0+4\right]x^2=0+4\)
\(\Leftrightarrow4x^2=4\)
\(\Leftrightarrow x^2=1\)
Phương trình có hai nghiệm là \(x=1,x=-1\).