Đáp án B

Ta có log(x + 2y) = log x + log y

<=> log 2 (x+2y) = log 2xy

<=> 2 (x+2y) = 2xy (*).

Đ ặ t   a = x > 0 b = 2 y > 0 , khi đó

* ⇔ 2 a + b = a b

và  P = a 2 1 + b + b 2 1 + a ≥ a + b 2 a + b + 2

Lại có  a b ≤ a + b 2 4 ⇒ 2 a + b ≤ a + b 2 4 ⇔ a + b ≥ 8 .

Đặt t = a + b, do đó

P ≥ f t = t 2 t + 2 .

X é t   h à m   s ố   f t = t 2 t + 2 t r ê n   [ 8 ; + ∞ )

c ó   f ' t = t 2 + 2 t t + 2 2 > 0 ; ∀ ≥ 8

Suy ra f(t) là hàm số đồng biến trên  [ 8 ; + ∞ )

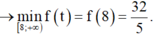
Vậy gía trị nhỏ nhất của biểu thức P là  32 5 .

Đáp án C

Theo đầu bài ta có: log ₂x+ log₂y=log₄(x+y) hay 2 log ₂(xy) =log₂(x+y)

Suy ra x+y=(xy) ² 

Đặt u= x+ y; v= xy  ta có điều kiện u²-4v≥0; u>0; v>0 .

Mà 

Ta có 

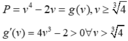
nên minP=  2 4 3 khi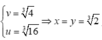 

Chọn A.

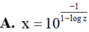
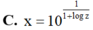
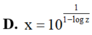
Đáp án D

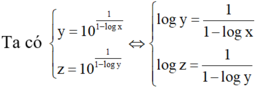
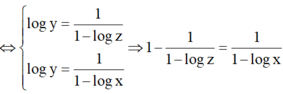
⇔ log   z - 1 log   z = 1 1 - log   x

⇔ 1 - log   x = log   z log   z - 1

⇔ log   x = - 1 log   z - 1 ⇔ x = 10 1 1 - log   z .

Chọn đáp án B.

Nếu một trong các số \(x+y-z;y+z-x;z+x-y\) bằng 0 thì cả 3 số đều bằng 0 và dẫn đến \(x=y=z=0\), mâu thuẫn

Từ giả thiết ta có : \(\begin{cases}x\log y\left(y+z-x\right)=y\log x\left(z+x-y\right)\\y\log z\left(z+x-y\right)=z\log y\left(x+y-z\right)\\z\log x\left(x+y-z\right)=x\log z\left(y+z-x\right)\end{cases}\)

Xét đẳng thức thứ nhất ta có :

                                               \(x\log y\left(y+z-x\right)=y\log x\left(z+x-y\right)\Leftrightarrow x\log y=y\log x.\frac{z+x-y}{y+z-x}\)                                                               \(\Leftrightarrow x\log y+y\log x=y\log x\left(\frac{z+x-y}{y+z-x}+1\right)\Leftrightarrow x\log y+z\log x=y\log x\frac{2z}{y+z-x}\)

Biến đổi tương tự với đẳng thức thứ hai ta có :

                                             \(y\log z+z\log y=z\log y\frac{2z}{z+z-y}\)

Ta thấy rằng : \(x^y.y^x=y^z.z^y\Leftrightarrow x\log y+y\log x=y\log z+z\log y\)

Do đó ta cần có :

                    \(y\log x\frac{2z}{y+z-x}=z\log y\frac{2z}{z+x-y}\Leftrightarrow y\log x\left(z+x-y\right)=x\log y\left(y+z-x\right)\), đúng

Do đó ta được : \(x^yy^x=y^z.z^y\)

Chứng minh tương tự ta có : \(y^zz^y=z^x.x^z\)

=> Điều phải chứng minh

Đáp án đúng : A