Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số y = - x 4 + 4 và y=-x+2
A. 9 2
B. 5 7
C. 8 3
D. 9
Những câu hỏi liên quan
Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số
y
−
x
2
+
4
v
à
y
-
x
+
2
A.
9
2
B.
5
7
C.
8
3
D. 9
Đọc tiếp
Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số y = − x 2 + 4 v à y = - x + 2
A. 9 2
B. 5 7
C. 8 3
D. 9
Đáp án là A
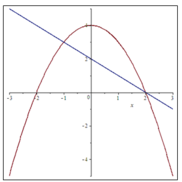
Hoành độ giao điểm của hai hàm số là
Đúng 0
Bình luận (0)
Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số y = - x 2 + 4 và y=-x+2
A. 9/2
B.5/7
C.8/3
D. 9
Tính Tính Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=x^2-4 và y =2x-4
Lời giải:
PT hoành độ giao điểm của 2 ĐTHS:
$x^2-4-(2x-4)=0\Leftrightarrow x^2-2x=0\Leftrightarrow x=0$ hoặc $x=2$
Diện tích hình phẳng giới hạn bởi 2 ĐTHS là:
\(\int ^2_0|x^2-4-(2x-4)|dx=\int ^2_0|x^2-2x|dx=\int ^2_0(2x-x^2)dx=\frac{4}{3}\)
Đúng 1
Bình luận (0)
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
y
x
2
-
x
+
1
và đường thẳng
y
x
+
4
.
Đọc tiếp
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x 2 - x + 1 và đường thẳng y = x + 4 .
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
y
x
2
-
x
+
1
và đường thẳng
y
x
+
4
. A. 9 B.
29
3
C.
23
3
D.
32
3
Đọc tiếp
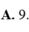
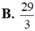
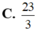
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x 2 - x + 1 và đường thẳng y = x + 4 .
A. 9
B. 29 3
C. 23 3
D. 32 3
Đáp án D.
Phương trình hoành độ giao điểm của hai đồ thị hàm số là:
Đúng 0
Bình luận (0)
Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số
y
x
3
-
4
x
, trục hoành và hai đường thẳng x -2, x4 là A. S 44 B. S 8. C. S 22 D. S36
Đọc tiếp
Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y = x 3 - 4 x , trục hoành và hai đường thẳng x= -2, x=4 là
A. S =44
B. S =8.
C. S =22
D. S=36
Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số
y
x
3
-
4
x
, trục hoành và hai đường thẳng x-2, x4 là:
Đọc tiếp
Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y = x 3 - 4 x , trục hoành và hai đường thẳng x=-2, x=4 là:
Cho hình phẳng giới hạn bởi đồ thị các hàm số
y
x
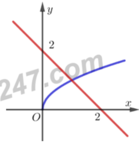
, đường thẳng y 2 - x và trục hoành. Diện tích hình phẳng sinh bởi hình phẳng giới hạn bởi các đồ thị trên là A.
7
6
.
B.
4
3
.
C.
5
6
.
D.
5
4
.
Đọc tiếp
Cho hình phẳng giới hạn bởi đồ thị các hàm số y = x , đường thẳng y = 2 - x và trục hoành. Diện tích hình phẳng sinh bởi hình phẳng giới hạn bởi các đồ thị trên là
A. 7 6 .
B. 4 3 .
C. 5 6 .
D. 5 4 .
Cho hàm số
y
9
-
4
x
2
có đồ thị là (C) . Tính diện tích hình phẳng giới hạn bởi đồ thị (C ) , trục Ox, hai đường thẳng
x
3
4
và
x
3
3
4
A.
3
π
8
B.
3...
Đọc tiếp
Cho hàm số y = 9 - 4 x 2 có đồ thị là (C) . Tính diện tích hình phẳng giới hạn bởi đồ thị (C ) , trục Ox, hai đường thẳng x = 3 4 và x = 3 3 4
A. 3 π 8
B. 3 π 4
C. 3 π 16
D. 3 π 2
