Các câu hỏi tương tự
Đặt (S) là diện tích hình phẳng giới hạn bởi đồ thị của hàm số
y
4
-
x
2
, trục hoành và đường thẳng
x
-
2
,
x
m
-
2
m
2
. Tìm giá trị của tham số m để
S
25
3...
Đọc tiếp
Đặt (S) là diện tích hình phẳng giới hạn bởi đồ thị của hàm số y = 4 - x 2 , trục hoành và đường thẳng x = - 2 , x = m - 2 < m < 2 . Tìm giá trị của tham số m để S = 25 3
A. 2
B. 3
C. 4
D. 1
Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số
y
x
2
+
2
x
+
1
trục hoành và hai đường thẳng x -1;x3 A. S64/3. B. S56/3. C. S37/3. D. S21.
Đọc tiếp
Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y = x 2 + 2 x + 1 trục hoành và hai đường thẳng x= -1;x=3
A. S=64/3.
B. S=56/3.
C. S=37/3.
D. S=21.
Gọi S là diện tích của hình phẳng giới hạn bởi đồ thị (C) của hàm số
y
x
4
+
x
2
, trục hoành, trục tung và đường thẳng
x
1
. Biết
S
a
5
+
b
,
a
,
b
∈
ℚ
. Tín...
Đọc tiếp
Gọi S là diện tích của hình phẳng giới hạn bởi đồ thị (C) của hàm số y = x 4 + x 2 , trục hoành, trục tung và đường thẳng x = 1 . Biết S = a 5 + b , a , b ∈ ℚ . Tính a + b
A. a + b = - 1
B. a + b = 1 2
C. a + b = 1 3
D. a + b = 13 3
Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y f(x) liên tục trên
a
;
b
trục hoành và hai đường thẳng
x
a
,
x
b
a
b
cho bởi công thức: A.
S
∫
a
b
f
x...
Đọc tiếp
Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y = f(x) liên tục trên a ; b trục hoành và hai đường thẳng x = a , x = b a < b cho bởi công thức:
A. S = ∫ a b f x d x
B. S = π ∫ a b f x d x
C. S = π ∫ a b f 2 x d x
D. S = ∫ a b f x d x
Hình phẳng giới hạn bởi đồ thị hàm số
y
f
x
liên tục trên đoạn [a;b], trục hoành và hai đường thẳng
x
a
,
x
b
a
≤
b
có diện tích S là A.
S
∫
a
b
f
x...
Đọc tiếp
Hình phẳng giới hạn bởi đồ thị hàm số y = f x liên tục trên đoạn [a;b], trục hoành và hai đường thẳng x = a , x = b a ≤ b có diện tích S là
A. S = ∫ a b f x d x
B. S = ∫ a b f x d x
C. S = ∫ a b f x d x
D. S = π ∫ a b f 2 x d x
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số
y
f
x
, trục hoành, đường thẳng x a, x b( như hình bên). Biết
∫
a
c
f
x
d
x
−
2
v
à
∫
c
b
f
x
d
x
5
. Hỏi S bằng ba...
Đọc tiếp
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f x , trục hoành, đường thẳng x = a, x = b( như hình bên). Biết ∫ a c f x d x = − 2 v à ∫ c b f x d x = 5 . Hỏi S bằng bao nhiêu?
A. 7
B. 5
C. 2
D. 3
Hình phẳng được giới hạn bởi đồ thị hàm số y f(x) liên tục trên đoạn [a;b] trục hoành và hai đường thẳng
x
a
,
x
b
a
≤
b
có diện tích S là: A.
S
∫
a
b
f
x...
Đọc tiếp
Hình phẳng được giới hạn bởi đồ thị hàm số y = f(x) liên tục trên đoạn [a;b] trục hoành và hai đường thẳng x = a , x = b a ≤ b có diện tích S là:
A. S = ∫ a b f x d x .
B. S = ∫ a b f x d x .
C. S = ∫ a b f x d x .
D. S = π ∫ a b f 2 x d x .
Hình phẳng được giới hạn bởi đồ thị hàm số y f(x) liên tục trên đoạn [a;b] trục hoành và hai đường thẳng x a, x b
a
≤
b
có diện tích S là A.
S
∫
a
b
f
x
d
x
B.
S
-
∫...
Đọc tiếp
Hình phẳng được giới hạn bởi đồ thị hàm số y= f(x) liên tục trên đoạn [a;b] trục hoành và hai đường thẳng x = a, x = b a ≤ b có diện tích S là
A. S = ∫ a b f x d x
B. S = - ∫ a b f x d x
C. S = ∫ a b f x d x
D. S = π ∫ a b f 2 x dx
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y f(x), trục hoành, đường thẳng x a, x b(như hình bên).Hỏi cách tính S nào dưới đây đúng? A.
S
∫
a
b
f
x
d
x
.
B.
S
∫
a
c
f
x
d...
Đọc tiếp
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành, đường thẳng x = a, x = b(như hình bên).
Hỏi cách tính S nào dưới đây đúng?
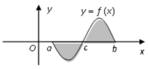
A. S = ∫ a b f x d x .
B. S = ∫ a c f x d x + ∫ c b f x d x .
C. S = − ∫ a c f x d x + ∫ c b f x d x .
D. S = ∫ a c f x d x + ∫ c b f x d x .




