Hàm số y = tan x liên tục trên khoảng nào sau đây:
A. 5 π 4 ; 7 π 4
B. − π 6 ; π 3
C. − π ; π 2
D. π 3 ; 5 π 6
Cho hàm số f ( x ) = tan x x ; x k h á c 0 ∧ x k h á c π 2 + k π ; k ∈ ℤ 0 ; x = 0 Hàm số y = f(x) liên tục trên các khoảng nào sau đây?
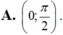
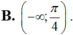
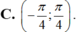
![]()
Chọn A.
TXĐ: 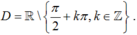 .
.
Với x = 0 ta có f(0) = 0.
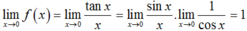 hay
hay ![]() .
.
Vậy hàm số gián đoạn tại x = 0.
Cho hàm số y=f(x) có đạo hàm liên tục trên ~ , hàm số y=f’(x) có đồ thị hàm số như hình dưới đây
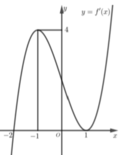
Hàm số y=f(x) đồng biến trên khoảng nào trong các khoảng sau:
A. (-∞;2); (1;+∞)
B. (-2;+∞)/{1}
C. (-2;+∞)
D. (-4;0)
Chọn C
Từ đồ thị hàm số y=f’(x) ta có bảng biến thiên cho hàm số y=f(x) như sau:
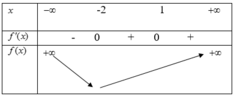
Nhìn vào bảng biến thiên ta thấy ngay trong khoảng (-2;+∞) thì hàm số y=f(x) đồng biến
Cho hàm số y=f(x) có đạo hàm liên tục trên khoảng (a;b) chứa x0. Mệnh đề nào sau đây là mệnh đề đúng?
A.Nếu f ' x 0 = 0 thì hàm số đạt cực trị tại x = x0.
B.Nếu hàm số đạt cực tiểu tại x = x0 thì f ' x 0 < 0 .
C.Nếu hàm số đạt cực trị tại x = x0 thì f ' x 0 = 0
D.Hàm số đạt cực trị tại x = x0 thì f ' x 0 = 0
Cho hàm số y = f(x) có đạo hàm liên tục trên khoảng (a;b) chứa x0. Mệnh đề nào sau đây là mệnh đề đúng?
A. Nếu f'(x0) = 0 thì hàm số đạt cực trị tại x = x0.
B. Nếu hàm số đạt cực tiểu tại x = x0 thì f'(x0) < 0.
C. Nếu hàm số đạt cực trị tại x = x0 thì f'(x0) = 0.
D. Hàm số đạt cực trị tại x = x0 khi và chỉ khi f'(x0) = 0.
Chọn C.
Đáp án A sai chẳng hạn xét hàm số f(x) = x 3 có f'(x) = 3 x 2 => f'(0) 0 nhưng hàm số không cực trị tại x = 0.
Đáp án B hiển nhiên sai vì ít nhất ta cần có f'(x) = 0 chứ không phải f'( x 0 ) < 0
Đáp án C hiển nhiên đúng.
Theo đáp án A thì D sai.
Cho hàm số f ( x ) = x 2 + 1 x 2 + 5 x + 6 Khi đó hàm số y = f(x) liên tục trên các khoảng nào sau đây?
A. (-3; 2).
B. (-2; +∞).
C. (-∞; 3).
D. (2; 3).
Chọn B.
Hàm số có nghĩa khi 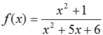 .
.
Vậy theo định lí ta có hàm số 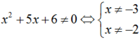 liên tục trên khoảng (-∞; -3); (-3; -2) và (-2; +∞).
liên tục trên khoảng (-∞; -3); (-3; -2) và (-2; +∞).
Cho hàm số y = f(x) có đạo hàm liên tục trên i. Đồ thị hàm số y = f’(x) như hình bên dưới
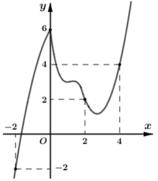
Hàm số g(x) = 2 f(x) - x 2 đồng biến trên khoảng nào trong các khoảng sau đây?
![]()
![]()
![]()
![]()
Cho hàm số y= f( x) có đạo hàm liên tục trên R. Đồ thị hàm số y= f’(x) như hình bên dưới
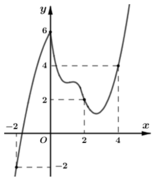
Hàm số g(x) = 2 . f(x) – x2 đồng biến trên khoảng nào trong các khoảng sau đây?
A. ( - ∞ ; - 2 )
B. (-2; 2)
C. (2; 4)
D. ( 2 ; + ∞ )
Cho hàm số y=f(x) liên tục trên khoảng (a,b) và x 0 ∈ a , b . Mệnh đề nào sau đây là đúng?

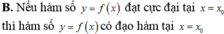
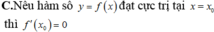
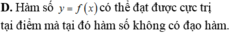
Cho hàm số y=f(x) liên tục trên R và có bảng xét dấu của hàm số f'(x) như sau:

Hàm số y=f(x) đồng biến trên khoảng nào dưới đây ?
A.(0;2)
B. 1 ; + ∞
C. 0 ; + ∞
D. - ∞ ; 0