Cho hình vuông ABCD cạnh a. M là điểm thuộc cạnh AB. Biểu thức D M → . B C → bằng
A. a 2
B. − 2 a 2
C. 2 a 2
D. - a 2
Đáp án D
D M → . B C → = D A → + A M → . B C → = D A → . B C → + A M → . B C →
= a . a . c os180 0 + A M . B C . c os 90 0 = − a 2 + 0 = − a 2
Cho Hình vuông ABCD cạnh a. M là trung điểm của AB . Tính giá trị biểu thức : (AB +AD)(BD+BC)
cho hình chóp s.abcd có đáy abcd là hình vuông cạnh a, \(SA=\sqrt{7}\) và vuông góc với đáy. lấy điểm M trên cạnh SC sao cho CM < a. gọi (C) là hình nón có đỉnh C, các điểm B, M, D thuộc mặt xung quanh, điểm A thuộc mặt đáy của hình nón. tính diện tích xung quanh của (C)
Cho hình vuông ABCD cạnh a. M là trung điểm của AB, Tính giá trị các biểu thức sau: ( A B → + A D → ) . ( B D → + B C → )
A. a2
B. –a2
C. 2a2
D. Đáp án khác
Chọn A.
Theo quy tắc hình bình hành ta có 
Do đó
(
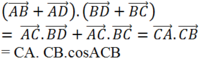
vì AC và BD vuông góc với nhau)
Mặt khác 
và theo định lý Pitago ta có:
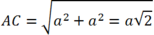
Suy ra 
Cho hình vuông ABCD cạnh là x(cm), lấy điểm M bất kì thuộc cạnh AB, Tia CM cắt DA tại E, tia Cz vuông góc với tia CE cắt AB tại F. Gọi N là trung điểm của đoạn thẳng EF
a/ Chứng minh: CE = CF.
b/ Chứng minh 4 điểm D, C, N, E thuộc một đường tròn.
c/ Chứng minh: khi điểm M chạy trên cạnh AB (M không trùng với A và B) thì điểm N luôn chạy trên một đường thẳng cố định
Cho hình vuông ABCD. Điểm M thuộc cạnh AB(M khác A và B). Tia CM cắt tia DA tại N. Vẽ Cx vuông góc với CM và cắt tia AB tại E. Gọi H là trung điểm của đoạn NE. Tìm vị trí của điểm M trên cạnh AB để diện tích tứ giác NACE bằng 15/8 diện tích hình vuông ABCD.
Mk chỉ nêu cách làm bạn tự triển khai nha!
CM \(\Delta ADC=\Delta CBE (g.c.g)\) (*)
(\(\angle C_1=\angle C_2\) cùng phụ với \(\angle ACB\))
\(\Rightarrow AC=CE\Rightarrow \Delta ACE \) cân tại C
\(\Rightarrow AB=CE\)
Từ (*) suy ra:
\(S_{ANEC}=S_{ACE}+S_{ANE}=S_{ABCD}+S_{ANE}\)
\(=\dfrac{1}{2}AB^2+\dfrac{1}{2}NA.2AB=\dfrac{1}{2}AB(AB+2NA)\)
Mà \( S_{ANCE}=\dfrac{15}{8} S_{ABCD}\) \(\Rightarrow \dfrac{15}{8}.\dfrac{1}{2} AB^2=\dfrac{1}{2}.AB(2AN+AB)\)
\(\Rightarrow 2AN+AB=\dfrac{15}{8}AB\) \(\Rightarrow \dfrac{NA}{AB}=\dfrac{7}{16}\)
CM \(\Delta NAM \) đồng dạng với \(\Delta CBM\) \((g.g)\)
\(\Rightarrow \dfrac{NA}{AB}=\dfrac{NA}{BC}=\dfrac{AM}{MB}=\dfrac{7}{16}\)
Vậy cần lấy M sao cho \(\dfrac{AM}{MB}=\dfrac{7}{16}\)
Cho hình vuông ABCD có 2 đường chéo cắt nhau tại E. Lấy I thuộc cạnh AB, M thuộc cạnh BC sao cho \(\widehat{IEM}=90^o\) ( I và M không trùng với các đỉnh của hình vuông).
a) C/m 4 điểm B,I,E,M cùng thuộc 1 đường tròn.
b) Tính \(\widehat{IME}\)c) Gọi N là giao điểm của tia AM và tia DC. K là giao điểm của tia BN và tia EM. C/m \(CK\perp BN\)
a) Xét tứ giác BIEM có
\(\widehat{IBM}\) và \(\widehat{IEM}\) là hai góc đối
\(\widehat{IBM}+\widehat{IEM}=180^0\)(\(90^0+90^0=180^0\))
Do đó: BIEM là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
⇔B,I,E,M cùng thuộc 1 đường tròn(đpcm)
b) Ta có: ABCD là hình vuông(gt)
nên BD là tia phân giác của \(\widehat{ABC}\)(Định lí hình vuông)
⇔BE là tia phân giác của \(\widehat{ABC}\)
⇔\(\widehat{ABD}=\dfrac{\widehat{ABC}}{2}=\dfrac{90^0}{2}=45^0\)
hay \(\widehat{IBE}=45^0\)
Ta có: BIEM là tứ giác nội tiếp(cmt)
nên \(\widehat{IBE}=\widehat{IME}\)(Định lí)
mà \(\widehat{IBE}=45^0\)(cmt)
nên \(\widehat{IME}=45^0\)
Vậy: \(\widehat{IME}=45^0\)
Bài 2. Cho hình vuông ABCD có cạnh là a, trên cạnh AB và BC lần lượt lấy các điểm M và N sao cho AM BN. Gọi K là giao điểm của AN và DM.
a/. Chứng minh rằng 4 điểm C, D, K, N cùng thuộc một đường tròn.
b/. Trong trường hợp M, N là trung điểm của AB và BC. Hãy xác định tâm của đường tròn này và tính bán kính của đường tròn theo a.
1) Cho\(\Delta ABC\)cân tại A. Trên cạnh AB lấy điểm E, trên cạnh AC lấy điểm E sao cho AD=CE. Gọi O là trung điểm của DE, K là giao điểm của AO và BC.C/m tứ giác ABCD là hình bình hành
2) Cho hình vuông ABCD có các cạnh bằng a. Gọi M,N là 2 điểm lần lượt trên cạnh 2 cạnh AB,AD sao cho chu vi \(\Delta AMN\)=2a. C/m: khoảng cách từ C đến đường thẳng MN không phụ thuộc vào vị trí của 2 điểm M,N trên cạnh AB, AD
