Cho hình vuông ABCD cạnh a. Mệnh đề nào sau đây sai? A. B. C. D.
Đọc tiếp
Cho hình vuông ABCD cạnh a. Mệnh đề nào sau đây sai?
A. 
B. 
C. 
D. 
Những câu hỏi liên quan
Cho hình vuông ABCD cạnh a. Mệnh đề nào sau đây sai? A.
A
B
→
.
A
D
→
0
B.
A
B
→
.
A
C
→
a
2
C.
A...
Đọc tiếp
Cho hình vuông ABCD cạnh a. Mệnh đề nào sau đây sai?
A. A B → . A D → = 0
B. A B → . A C → = a 2
C. A B → . C D → = a 2
D. A B → + C D → + B C → . A D → = a 2
Cho hình vuông ABCD cạnh a . Hỏi mệnh đề nào sau đây sai? A. B. C. D.
Đọc tiếp
Cho hình vuông ABCD cạnh a . Hỏi mệnh đề nào sau đây sai?
A. 
B. 
C. 
D. 
Cho hình vuông ABCD cạnh a. Hỏi mệnh đề nào sau đây đúng
A. 
không phụ thuộc vào vị trí điểm M.
B. Độ dài vectơ u là 2.
C. Cả A và B sai.
D .cà A và B đúng
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, ABC
60
0
. Hai mặt bên (SAD) và (SAB) cùng vuông góc với đáy (ABCD) . Cạnh SBa
2
. Mệnh đề nào dưới đây sai? A.
S
A
B
C
D...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, ABC = 60 0 . Hai mặt bên (SAD) và (SAB) cùng vuông góc với đáy (ABCD) . Cạnh SB=a 2 . Mệnh đề nào dưới đây sai?
A. S A B C D = a 2 3 2
B. SC=a 2
C. (SAC ) ⊥ (SBD).
D. V S . A B C D = 5 3 a 3 12
Cho hình chóp S.ABCD, tứ giác ABCD đáy là hình thang vuông tại A và B, S vuông góc với mặt phẳng (ABCD). Biết AB2CD2AD. Mệnh đề nào sau đây sai?
Đọc tiếp
Cho hình chóp S.ABCD, tứ giác ABCD đáy là hình thang vuông tại A và B, S vuông góc với mặt phẳng (ABCD). Biết AB=2CD=2AD. Mệnh đề nào sau đây sai?
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a,
A
B
C
^
60
0
. Hai mặt bên (SAD) và (SAB) cùng vuông góc với đáy (ABCD) . Cạnh
S
B
a
2
. Mệnh đề nào dưới đây sai? A.
S
A
B
C
D...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, A B C ^ = 60 0 . Hai mặt bên (SAD) và (SAB) cùng vuông góc với đáy (ABCD) . Cạnh S B = a 2 . Mệnh đề nào dưới đây sai?
A. S A B C D = a 2 3 2
B. S C = a 2
C. S A C ⊥ S B D
D. V S . A B C D = a 3 3 12
Cho hình vuông ABCD tâm O. Hỏi mệnh đề nào sau đây sai? A. B. C. D.
Đọc tiếp
Cho hình vuông ABCD tâm O. Hỏi mệnh đề nào sau đây sai?
A. 
B. 
C. 
D. 
Chọn C.
+ Phương án A: ABCD là hình vuông nên mOa và OB vuông góc với nhau
suy ra 
loại A.
+ Phương án B: OA và OC vuông góc với nhau nên 
và 
suy ra 
loại B.
+ Phương án C: 
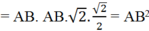
Do 
là 2 vecto ngược hướng nên 
suy ra :
Đúng 0
Bình luận (0)
Cho hình chóp S. ABCD có đáy ABCD là hình vuông và SA vuông góc đáy. Mệnh đề nào sau đây sai? A.
B
C
⊥
S
A
B
B.
A
C
⊥
S
B
D
C.
B
D
⊥
S
A
C
D.
C
D
⊥...
Đọc tiếp
Cho hình chóp S. ABCD có đáy ABCD là hình vuông và SA vuông góc đáy. Mệnh đề nào sau đây sai?
A. B C ⊥ S A B
B. A C ⊥ S B D
C. B D ⊥ S A C
D. C D ⊥ S A D
trang 127 SGK Toán 11 tập 1 - Chân trời sáng tạo
17 tháng 7 2023 lúc 22:06
Cho tam giác \(ABC\). Lấy điểm \(M\) trên cạnh \(AC\) kéo dài (Hình 1). Mệnh đề nào sau đây là mệnh đề sai?
A. \(M \in \left( {ABC} \right)\).
B. \(C \in \left( {ABM} \right)\).
C. \(A \in \left( {MBC} \right)\).
D. \(B \in \left( {ACM} \right)\).
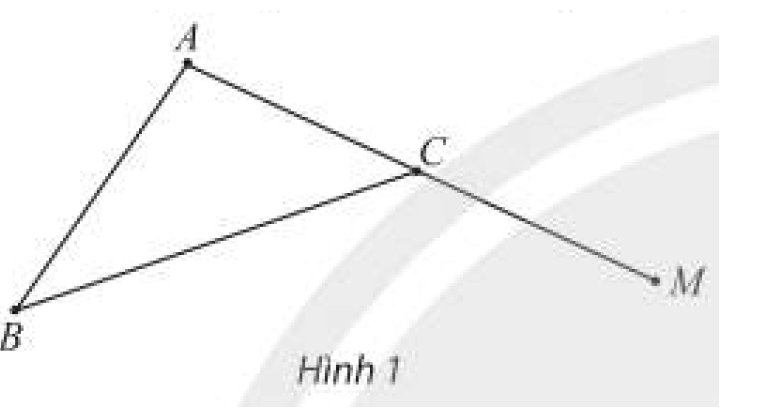
\(\left. \begin{array}{l}M \in AC\\AC \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow M \in \left( {ABC} \right)\). Vậy mệnh đề A đúng.
\(\left. \begin{array}{l}C \in AM\\AM \subset \left( {ABM} \right)\end{array} \right\} \Rightarrow C \in \left( {ABM} \right)\). Vậy mệnh đề B đúng.
\(\left. \begin{array}{l}A \in CM\\CM \subset \left( {MBC} \right)\end{array} \right\} \Rightarrow A \in \left( {MBC} \right)\). Vậy mệnh đề C đúng.
Vậy mệnh đề D sai.
Chọn D.
Đúng 0
Bình luận (0)