Cho x O y ^ = 120 o . Vẽ O x ' ⊥ O x ; O y ' ⊥ O y sao cho tia Ox',Oy' nằm giữa hai tia Ox, Oy
Kẻ Om và On là tia phân giác của các góc xOy' và x'Oy. Khi đó
A. Om ⊥ On
B. Om ⊥ Ox'
C. On ⊥ Oy'
D. Ox ⊥ Oy
Cho x O y ^ = 120 ° . Lấy điêm A trên tia Ox. Trên cùng nửa mặt phẳng bờ Ox chứa tia Oy vẽ tia At sao cho O A t ^ = 60 ° .
a) Chứng minh At // Oy.
b) Gọi On, Om lần lượt là 2 tia phân giác của x O y ^ và x A t ^. Chứng minh On // Am Giúp mk với
Cho hai tia Oy oz F cùng nằm trên một nửa mặt phẳng có bờ chứa tia Oy x biết góc x o z = 30 độ góc x o c bằng 120 độ tính số đo của góc y o z Vẽ tia phân giác của góc y o z tính số đo của góc x o t
câc bạn ơi giúp mình với:
cho đoạn thẳng xy cắt đoạn thặng x' y' tại o biết góc x'=120 độ.
a) vẽ hình
b) tính các góc trên hình vẽ
Xin lỗi nha, thật ra mink mới học có lớp 5 thôi à nên MINK thế giúp bn làm bài toán này, mong bn tha thứ cho mink
Cho hình vẽ
O'x' // Ox , O'y cắt Ox tại k . tính x'O'y' và x'O'k theo O
Cho $\widehat{x O y}=90^{\circ}$, vẽ hai tia $O A,$ $O B$ ở trong góc đó sao cho $\widehat{x O A}=\widehat{y O B}=60^{\circ}$. Trên nửa mặt phẳng bờ $O x$ chứa tia $O y$, vẽ tia $O M$ sao cho $O y$ là tia phân giác của $\widehat{M O B}$.
a) Chứng minh tia $O A$ là tia phân giác $\widehat{y O B}$, tia $O B$ là tia phân giác $\widehat{x O A}$.
b) Chứng minh $O M \perp O A$.
cửa hàng bán được một tạ rưỡi gẹo tẻ và gạo nếp ; trong đó 25% là gạo nếp. hỏi của hàng bán mỗi loại bao nhiêu ki-lô-gam gạo
a)xOy=xOA+AOy(vì là 2 góc kề bù)
90=60+AOy
AOy=90-60
AOy=30
=> OA là tia phân giác của yOB
xOy=yOB+BOA(vì là 2 góc kề bù)
90=60+BOA
BOA=90-60
BOA=30
=>OB là tia phân giác của xOA(vì tia phân giác bằng 60:2=30)
b)
Cho hình vẽ :
O'x' song song với Ox , O'y cắt Ox tại k . Tính góc x'O'y' và góc x'O'k theo góc O
Cho góc $\widehat{x O y}=140^{\circ}$. Ở ngoài của góc, vẽ hai tia $O A$ và $O B$ sao cho $O A \perp O x,$ $O B \perp O y$. Gọi $O M$ là tia phân giác của $\overline{x O y}$ và $O M'$ là tia đối của tia $OM$.
a) Chứng minh $O M'$ là tia phân giác của $\widehat{A O B}$.
b) Tính số đo góc $\widehat{xOB}$.
a) Ta có: \(\widehat{xOy}=140^0\)
\(\widehat{xOA}=\widehat{yOB}=90^0\) ( do \(OA\perp Ox,OB\perp Oy\) )
\(\Rightarrow\widehat{AOB}=360-\left(\widehat{xOy}+\widehat{xOA}+\widehat{yOB}\right)\)
\(\Leftrightarrow\widehat{AOB}=360^0-\left(140^0+90^0+90^0\right)\)
\(\Leftrightarrow\widehat{AOB}=40^0\)
\(OM\) là tia phân giác của \(\widehat{xOy}\)
\(\Rightarrow\widehat{xOM}=\widehat{MOy}=\dfrac{1}{2}\widehat{xOy}=\dfrac{1}{2}.140^0=70^0\)
\(OM'\) là tia đối của \(OM\Rightarrow\widehat{MOM'}=180^0\)
Mà \(OA\) nằm ngoài \(\widehat{xOy}\) và \(OA\perp Ox\) nên \(\widehat{MOM'}=\widehat{MOx}+\widehat{xOA}+\widehat{AOM'}\)
Do đó \(\widehat{AOM'}=\widehat{MOM'}-\left(\widehat{MOx}+\widehat{xOA}\right)\) \(\Rightarrow\widehat{AOM'}=180^0-\left(70^0+90^0\right)=20^0\) \(\left(1\right)\)
Mặt khác \(Oy\) nằm giữa \(OB\) và \(OM\) nên \(\widehat{MOB}=\widehat{MOy}+\widehat{yOB}=70^0+90^0=160^0\)
\(\Rightarrow\widehat{MOB}< \widehat{MOM'}\)
Do đó \(OB\) và \(Oy\) nằm cùng nửa mặt phẳng bờ \(MM'\)
\(Ox\) nằm giữa \(OA\) và \(OM\) nên\(\widehat{MOA}=\widehat{MOx}+\widehat{xOA}=70^0+90^0=160^0\)
\(\Rightarrow\widehat{MOA}< \widehat{MOM'}\)
Do đó tia \(OA\) và \(Ox\) nằm cùng nửa mặt phẳng bờ \(MM'\)
Nên \(OM'\) nằm giữa \(OA\) và \(OB\)
\(\Rightarrow\widehat{AOB}=\widehat{AOM'}+\widehat{M'OB}\Rightarrow\widehat{M'OB}=\widehat{AOB}-\widehat{AOM'}=40^0-20^0=20^0\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) ta có: \(\widehat{M'OB}=\widehat{AOM'}=20^0=\dfrac{1}{2}\widehat{AOB}\)
Suy ra \(OM'\) là tia phân giác của góc \(\widehat{AOB}\)
b) Ta có: \(\widehat{MOx}< \widehat{MOA}< \widehat{MOM'}\) nên \(OA\) nằm giữa \(Ox\) và \(OM'\)
Mà \(OM'\) là tia phân giác của góc \(\widehat{AOB}\)
Suy ra \(OA\) nằm giữa \(Ox\) và \(OB\)
Vậy \(\widehat{xOB}=\widehat{xOA}+\widehat{AOB}=90^0+40^0=130^0\)
a) Suy ra OM' là tia phân giác của góc AOB.
b) Vậy góc xOB = góc xOA + góc AOB = 90o + 40o = 130o.
Cho góc Nhọn Xoy , lấy điểm O' bất kỳ - 1) Vẽ X' , O' , Y' là góc nhọn sao cho : O'Y'// Oy , O'x' // Ox . Dùng thước đo góc để so sánh Xoy và x'o'y'
2 ) Vẽ X'o'y' Là góc tù sao cho : O'X' // Ox , O'y // Oy , Dùng thước đo góc để xét mối quan hệ 2 góc Xoy và x'o'y'
1, Góc xOy = x'O'y'
2, 2 góc đều là góc tù,có cùng số đo độ
Cho hai góc nhọn xOy và x'O'y' có các cạnh tương ứng Ox // O'x' , Oy // O'y'. Vẽ các tia Oz và O'z' lần lượt là phân giác của góc xOy và x'O'y'. Chứng tỏ :
a) Hai góc xOy và x'O'y' bằng nhau.
b) Oz // O'z'.
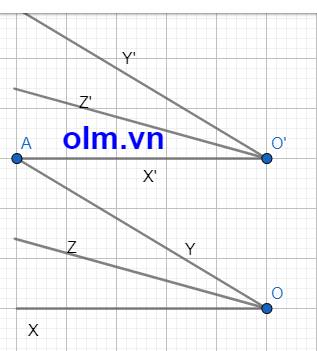
a,Kéo dài OY cắt O'X' tại A ta có:
\(\widehat{XOY}\) = \(\widehat{XOA}\) = \(\widehat{OAO'}\) (so le trong) (1)
\(\widehat{Y'O'X'}\) = \(\widehat{Y'O'A}\) = \(\widehat{OAO'}\) (so le trong) (2)
Kết hợp (1) Và (2) ta có:
\(\widehat{XOY=}\) \(\widehat{X'O'Y'}\) (đpcm)
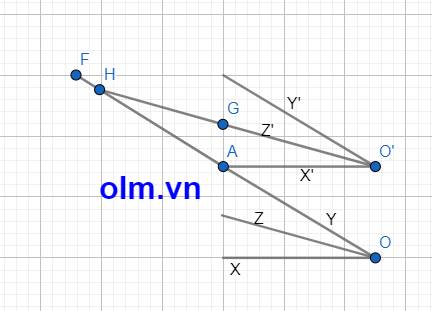
b, Kéo dài OY cắt O'Z' tại H
\(\widehat{ZOA}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\) (vì OZ là phân giác của góc XOY
\(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{X'O'Y'}\) (vì OY là phân giác của góc X'O'Y')
Mặt khác ta có \(\widehat{OAO'}\) = \(\widehat{HO'A}\) + \(\widehat{AHO'}\) (góc ngoài tam giác bằng tổng hai góc trong không kề với nó)
\(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\) ⇒ \(\widehat{AHO'}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\)
⇒ \(\widehat{ZOA}\) = \(\widehat{AHO'}\) (hai góc này ở vị trí so le trong)
⇒ OZ // O'Z' (đpcm)
cho góc nhon xOy và 1 điểm O'.hãy vẽ 1 góc nhọn x'O'y'có O'x'//Ox và O'y'//Oy.Hãy đo xem 2 góc xOy và x'O'y' có bằng nhau không?