Không vẽ hình, hỏi hệ phương trình sau có bao nhiêu nghiệm:
- 2 x + 5 y = 10 16 x - 40 y = 20
A. Vô số nghiệm
B. 0
C.1
D. 2
Không cần vẽ hình, cho biết mỗi hệ phương trình sau có bao nhiêu nghiệm?
y = 2 x + 10 y = x + 100
A. 1
B. Vô số
C. 0
D. 2
Đáp án A
+ Tập nghiệm của phương trình y = 2x + 10 được biểu diễn bởi đường thẳng d 1 :y = 2x + 10.
+ Tập nghiệm của phương trình y = x + 100 được biểu diễn bởi đường thẳng d 2 : y = x + 100.
Lại có: hệ số góc của hai đường thẳng d 1 ; d 2 khác nhau (2 ≠ 1) nên hai đường thẳng này cắt nhau.
Suy ra, hệ phương trình đã cho có nghiệm duy nhất.
Không vẽ hình, hãy cho biết hệ phương trình sau có bao nhiêu nghiệm.
x − 2 y + 10 = 0 − 3 x + 6 y − 30 = 0
A. 1
B. Vô số
C. 0
D. 2
Đáp án B
Ta có:
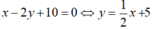
Nên tập nghiệm của phương trình x – 2y + 10 = 0 được biểu diễn bởi đường thẳng (d1):
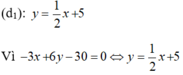
Nên tập nghiệm của phương trình -3x +6y – 30= 0 được biểu diễn bởi đường thẳng (d2):
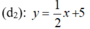
Do đó, nên hệ phương trình đã cho có vô số nghiệm.
Không giải các hẹ phương trình sau, hãy cho biết mỗi hệ phương trình có bao nhiêu nghiệm? Vì sao?
![]()
![]()
![]()
Cho hàm số y=f(x) có đồ thị như hình vẽ. Hỏi phương trình \(f\left(x^3-2x^2+14x+\sqrt{17}\right)=\sqrt{17}\) có bao nhiêu nghiệm thực?
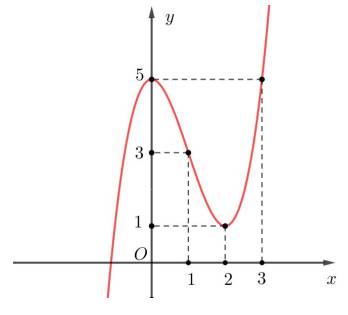
(1) Vẽ đồ thị của phương trình y = 2x-5 từ x = -3 đến x = 3.
(2) Sử dụng biểu đồ trong (a) để trả lời các câu hỏi sau:
(a) (-2, -9) có phải là nghiệm của phương trình không?
(b) Điểm A (2, a) nằm trên đồ thị. Giá trị của a là bao nhiêu?
(c) Điểm B (b, –7) nằm trên đồ thị. Giá trị của b là bao nhiêu?
Lời giải:
1.
$x=-3$ thì $y=2.(-3)-5=-11$. Ta có điểm $M(-3; -11)$
$x=3$ thì $y=2.3-5=1$. Ta có điểm $I(3;1)$
Nối hai điểm trên là được.
2.
a. Điểm $C(-2;-9)$ thuộc đồ thị hàm số trên
b. $A(2;a)$ thuộc đồ thị nên $y_A=2x_A-5$ hay $a=2.2-5=-1$
c. $B(b, -7)$ thuộc đồ thị nên $y_B=2x_B-5$ hay $-7=2b-5$
$2b=-2\Rightarrow b=-1$
(2) bạn tự vẽ
(a) giả sử y = 2x - 5 đi qua (-2;-9) <=> -4 - 5 = -9 ( tm )
vậy (-2;-9) là nghiệm pt trên
(b) y = 2x - 5 đi qua A(2;a) <=> a = 2.2 - 5 = -1
(c) y = 2x - 5 đi qua B(b;-7) <=> 2b - 5 = -7 <=> b = -1
Cho hàm số f(x) có bảng biến thiên như hình vẽ sau:

Phương trình f 2 sin x = 3 có bao nhiêu nghiệm trên đoạn 0 ; 5 π 6 .
A. 3.
B. 2.
C. 4.
D. 5.
Cho hàm số y = f x có đồ thị như hình vẽ. Hỏi phương trình m = f x + 1 với m<2 có bao nhiêu nghiệm?
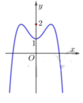
A. 3
B. Vô nghiệm
C. 4
D. 2
Đáp án D
m = f x + 1 ⇔ f x = m − 1
Do m < 2 ⇒ m − 1 < 1 nên PT f x = m − 1 có 2 nghiệm phân biệt.
Trong các khẳng định sau, khẳng định nào đúng?
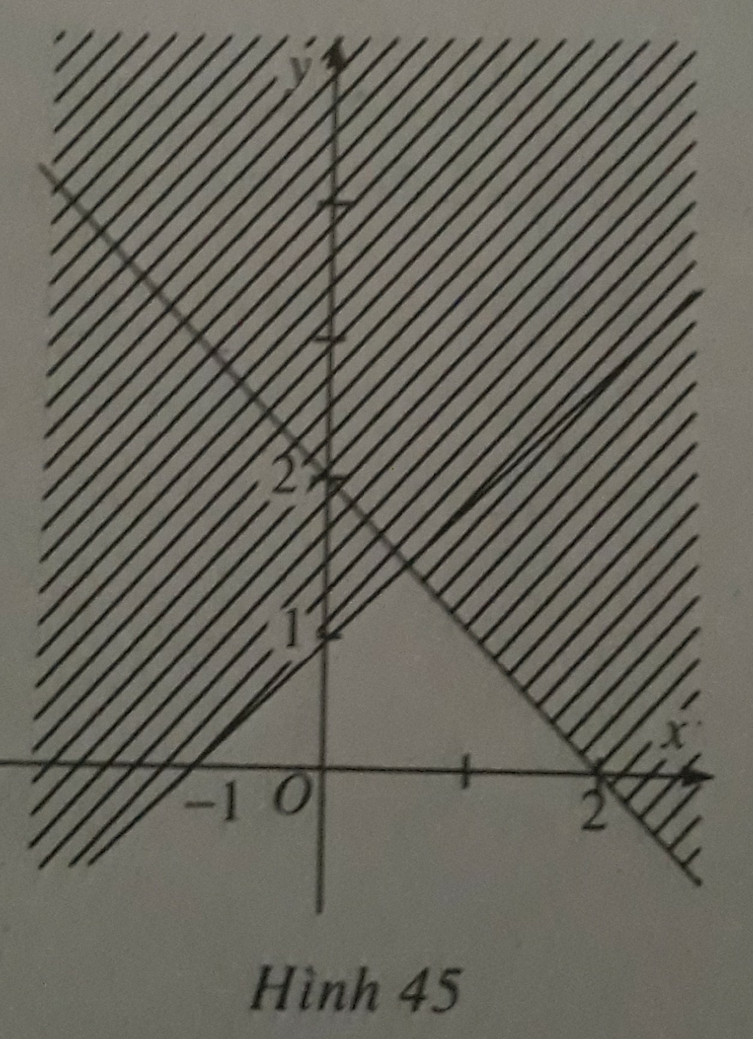
A. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình x + y ≤ 2.
B. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình![]()
và (x; y) = (-1; 1) là một nghiệm của hệ.
C. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình ![]() và (x; y) = (-2; 1) là một nghiệm của hệ.
và (x; y) = (-2; 1) là một nghiệm của hệ.
D. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình 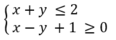 và (x; y) = (1; 0) là một nghiệm của hệ.
và (x; y) = (1; 0) là một nghiệm của hệ.
Cho hàm số y=f(x) liên tục trên đoạn [-2;2], và có đồ thị là đường cong như trong hình vẽ bên. Hỏi phương trình f x - 1 = 2 - x có bao nhiêu nghiệm phân biệt trên đoạn [-2;2]
A. 2
B. 5
C. 4
D. 3