giúp mình câu này nha rất gâ rồi

Những câu hỏi liên quan
giúp mình câu này nha mình đang rất gấp rồi
Đọc tiếp
giúp mình câu này nha mình đang rất gấp rồi
\(i=i'\)
\(\Rightarrow\)Góc hợp bởi tia phản xạ với mặt gương bằng góc hợp bởi tia tới và mặt gương
\(\Rightarrow\)SI năm phương nằm ngang một góc 45o
Đúng 3
Bình luận (0)
giúp mình câu này nha rất gấp rồi
Đọc tiếp
giúp mình câu này nha rất gấp rồi
giúp mình câu này nha khẩn cấp , mình rất gấp rồi
Đọc tiếp
giúp mình câu này nha khẩn cấp , mình rất gấp rồi
àm ơn làm ơn hãy giúp mình câu này nha mình rất gấp rồi, mình thề sẽ quỳ gối trước bạn nào giúp mình

a: Xét ΔABM và ΔCDM có
MA=MC
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔABM=ΔCDM
Đúng 1
Bình luận (0)
a) Xét tam giác ABM và tam giác CDM có:
+ AM = CM (cho M là trung điểm của AC).
+ BM = DM (gt).
+ \(\widehat{AMB}=\widehat{CMD}\) (2 góc đối đỉnh).
\(\Rightarrow\) Tam giác ABM = Tam giác CDM (c - g - c).
b) Ta có: \(\widehat{BAM}=\widehat{DCM}\) (Tam giác ABM = Tam giác CDM).
Mà 2 góc này ở vị trí so le trong.
\(\Rightarrow\) AB // CD (dhnb).
c) Xét tam giác ABN và tam giác ECN có:
+ BN = CN (N là trung điểm của BC).
+ \(\widehat{ANN}=\widehat{ENC}\) 2 góc đối đỉnh).
+ \(\widehat{ABN}=\widehat{ECN}\) (do AB // CD).
\(\Rightarrow\) Tam giác ABN = Tam giác ECN (g - c - g).
\(\Rightarrow\) CE = AB (2 cạnh tương ứng).
Mà AB = CD (Tam giác ABM = Tam giác CDM).
\(\Rightarrow\) CE = CD (cùng = AB).
\(\Rightarrow\) C là trung điểm của DE (đpcm).
d) Xét tam giác BDE có:
+ M là trung điểm của BD (do MD = MB).
+ C là trung điểm của DE (cmt).
\(\Rightarrow\) MC là đường trung bình.
\(\Rightarrow\) MC // BE và MC = \(\dfrac{1}{2}\) BE (Tính chất đường trung bình trong tam giác).
Lại có: MC = \(\dfrac{1}{2}\) MF (do MC = MF).
\(\Rightarrow\) BE = MF.
Xét tứ giác BMEF có:
+ BE = MF (cmt).
+ BE // MF (MC // BE; C thuộc MF).
\(\Rightarrow\) Tứ giác BMEF là hình bình hành (dhnb).
\(\Rightarrow\) ME cắt BF tại trung điểm của mỗi đường (Tính chất hình bình hành).
Mà O là trung điểm của ME (gt).
\(\Rightarrow\) O là trung điểm của BF.
\(\Rightarrow\) 3 điểm B; O; F thẳng hàng (đpcm).
Đúng 1
Bình luận (0)
Có bạn nào biết làm thi giúp mfinh câu này nha mình đang cần gấp 9 giờ là mình phải nộp cho thầy rồi thầy này cực khó tính nếu được mình cảm ơn rất rất nhiều
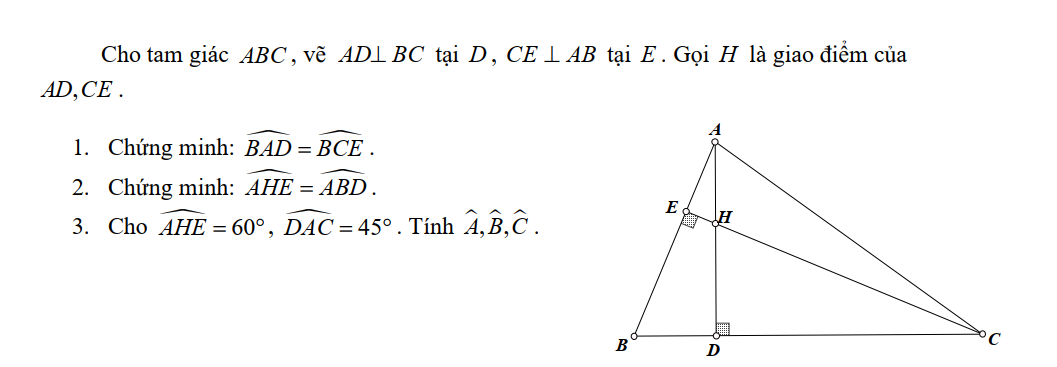
1: Ta có: \(\widehat{BAD}+\widehat{B}=90^0\)
\(\widehat{BCE}+\widehat{B}=90^0\)
Do đó: \(\widehat{BAD}=\widehat{BCE}\)
2: Ta có: \(\widehat{AHE}+\widehat{BAD}=90^0\)
\(\widehat{ABD}+\widehat{BAD}=90^0\)
Do đó: \(\widehat{AHE}=\widehat{ABD}\)
Đúng 1
Bình luận (1)
câu 3:
Xét tam giác AEH vuông tại E: góc AHE+ góc EAH= 90 độ
60 độ +góc EAH=90 độ
góc EAH=30 độ (1)
Ta có: góc A= góc EAH+ góc HAC= 30 độ +45 độ= 75 độ
Xét tam giác ADB vuông tại D có: góc B + góc EAH= 90 độ
góc B= 90 độ - 30 độ= 60 độ
lại có: góc BAC+ góc B + góc ACB= 180 độ (đ/ lý tổng ba góc trong 1 tam giác)
=> góc ACB= 180 độ-( 75 độ + 60 độ )= 45 độ
Đúng 0
Bình luận (1)
Có bạn nào biết làm câu này thì giúp mình nha mình đang cần cực gấp 11 giờ mình phải nộp cho thầy rồi(chỉ cònn 2 tiếng gấp lắm rồi) nếu được thì mình cảm ơn rất rất nhiều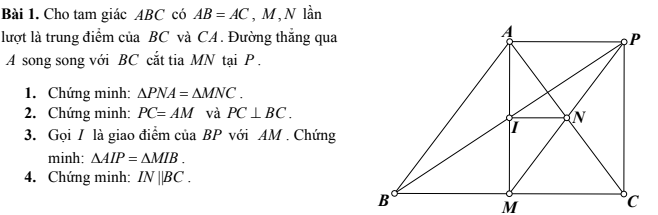
4: Xét ΔAMC có
I là trung điểm của AM
N là trung điểm của AC
Do đó: IN là đường trung bình của ΔAMC
Suy ra: IN//MC
hay IN//BC
Đúng 0
Bình luận (1)
Có bạn nào biết làm câu này thì giúp mình nha mình đang cần cực gấp 11 giờ mình phải nộp cho thầy rồi(chỉ cònn 2 tiếng gấp lắm rồi) nếu được thì mình cảm ơn rất rất nhiều
1: Xét ΔABC có AB=AC
nên ΔABC cân tại A
Suy ra: \(\widehat{B}=\widehat{C}\)
Ta có: ΔBAC cân tại A
mà AH là đường trung tuyến ứng với cạnh đáy BC
nên AH là đường cao ứng với cạnh BC
Đúng 0
Bình luận (0)
Có bạn nào biết làm câu này thì giúp mình nha mình đang cần cực gấp 11 giờ mình phải nộp cho thầy rồi(chỉ cònn 2 tiếng gấp lắm rồi) nếu được thì mình cảm ơn rất rất nhiều
1. Tam giác AOC và tam giác BOD có: AO = BO; CO = DO: góc AOC = góc BOD (đối đỉnh)
--> tam giác AOC = tam giác BOD (c.g.c)
--> góc ACO = góc ODB
Mà 2 góc này ở vị trí so le trong
--> AC // BD
Đúng 0
Bình luận (0)
b) Tam giác ACD và tam giác BDC có: CD chung; AC = BD (do tam giác AOC = tam giác BOD); góc ACO = góc ODB (câu a)
--> tam giác ACD = tam giác BDC
Đúng 0
Bình luận (0)
c) tam giác ACD = tam giác BDC (câu b)
--> góc DBC = góc CAD
Tam giác DAE và tam giác CBF có: góc DBC=góc CAD; AE = BF; BC = AD
--> tam giác DAE = tam giác CBF (c.g.c)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
ó bạn nào biết làm câu này thì giúp mình nha mình đnag cần gấp trước 6 giờ rất gấp rồi mình cảm on trước
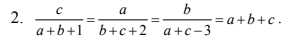 tìm a, b, c
tìm a, b, c
Áp dụng t/c dtsbn:
\(a+b+c=\dfrac{c}{a+b+1}=\dfrac{a}{b+c+2}=\dfrac{b}{a+c-3}=\dfrac{a+b+c}{2a+2b+2c}=\dfrac{1}{2}\\ \Rightarrow\left\{{}\begin{matrix}a+b+c=\dfrac{1}{2}\\2c=a+b+1\\2a=b+c+2\\2b=a+c-3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a+b+c+1=3c\\a+b+c+2=3a\\a+b+c-3=3b\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}3c=\dfrac{3}{2}\\3a=\dfrac{5}{2}\\3b=-\dfrac{5}{2}\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}c=\dfrac{1}{2}\\a=\dfrac{5}{6}\\b=-\dfrac{5}{6}\end{matrix}\right.\)
Đúng 3
Bình luận (0)















