Xét tam giác ABC vì BC là cạnh lớn nhất nên AB < BC và AC < BC.

Mà ta lại có: AC > 0 và AB > 0 hay 0 < AC và 0 < AB

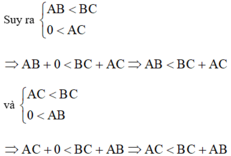
⇒ Đpcm

a = 1

a) ∆ABC có cạnh BC lớn nhất nên chân đường cao kẻ từ A phải nằm giữa B và C

=> HB + HC = BC

∆AHC vuông tại H => HC < AC

∆AHB vuông tại H => HB < AB

Cộng theo vế hai bất đẳng thức ta có:

HB + HC < AC + AB

Hay BC < AC + AB

b) BC là cạnh lớn nhất nên suy ra AB < BC và AC < BC

Do đó AB < BC + AC; AC < BC +AB

(cộng thêm AC hoặc AB vào vế phải của bất đẳng thức)

a) ∆ABC có cạnh BC lớn nhất nên chân đường cao kẻ từ A phải nằm giữa B và C

=> HB  + HC = BC

∆AHC vuông tại H => HC < AC

∆AHB vuông tại H => HB < AB

Cộng theo vế hai bất đẳng thức ta có:

HB + HC < AC + AB

Hay BC < AC + AB

b) BC là cạnh lớn nhất nên suy ra AB < BC và AC < BC

Do đó AB < BC + AC; AC < BC +AB

(cộng thêm AC hoặc AB vào vế phải của bất đẳng thức)

\(A^2=\left(x-y\right)^2=\left(1.x+\dfrac{1}{2}.\left(-2y\right)\right)^2\le\left(1+\dfrac{1}{4}\right)\left(x^2+4y^2\right)=\dfrac{5}{4}\)

\(\Rightarrow A\le\dfrac{\sqrt{5}}{2}\)

Dấu "=" xảy ra khi \(\left(x;y\right)=\left(-\dfrac{2\sqrt{5}}{5};\dfrac{\sqrt{5}}{10}\right);\left(\dfrac{2\sqrt{5}}{5};-\dfrac{\sqrt{5}}{10}\right)\)

Theo giả thiết, tam giác ABC có độ dài cạnh BC là lớn nhất nên chân đường vuông góc kẻ từ A đến cạnh BC chắn chắn phải nằm giữa B và C.

Suy ra H nằm giữa B và C.

⇒ HB + HC = BC

+) Xét tam giác AHB vuông tại H ta có: HB < AB (1) (vì trong tam giác vuông cạnh huyền là cạnh lớn nhất)

+) Xét tam giác AHC vuông tại H ta có: HC < AC (2) (vì trong tam giác vuông cạnh huyền là cạnh lớn nhất)

Lấy (1) + (2) ta được:

HB + HC < AB + AC

Mà HB + HC = BC suy ra BC < AB + AC hay AB + AC > BC

a) Xét tam giác vuông AHC có AC là cạnh lớn nhất ( cạnh lớn nhất trong tam giác vuông)                                    => AC>HC (1)                                                                                                                                                 Xét tam giác vuông AHB có AB là cạnh lớn nhất (canh lớn nhất trong tam giác vuông)                                        =>AB>HB  (2)                                                                                                                                                 Ta có : HC+HB+BC ( H nằm giũa A và C)  (3)                                                                                                  Từ (1) , (2) và (3) => AC+AB>BC                                                                                                                    b)Xét tam giác ABC có BC là cạnh lớn nhất(gt)                                                                                               =>BC>AB                                                                                                                                                  Ta có : AC>0 => BC+AC>AB                                                                                                                       Xét tam giác ABC có BC là cạnh lớn nhất (gt) =>BC>AC                                                                             Vì AB>0=>BC+AB>AC