Xét tam giác ABC vì BC là cạnh lớn nhất nên AB < BC và AC < BC.
Mà ta lại có: AC > 0 và AB > 0 hay 0 < AC và 0 < AB
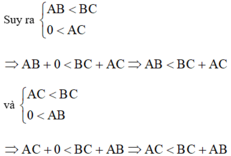
⇒ Đpcm
Xét tam giác ABC vì BC là cạnh lớn nhất nên AB < BC và AC < BC.
Mà ta lại có: AC > 0 và AB > 0 hay 0 < AC và 0 < AB
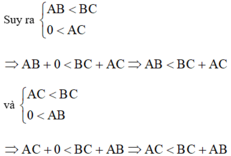
⇒ Đpcm
Một cách chứng minh khác của bất đẳng thức:
Cho tam giác ABC. Giả sử BC là cạnh lớn nhất. Kẻ đường thẳng vuông góc AH đến đường thẳng BC.
a) Dùng nhận xét về cạnh lớn nhất trong tam giác vuông để chứng minh AB+ AC> BC.
b) Từ giả thiết về cạnh BC, hãy suy ra hai bất đẳng thức tam giác còn lại.
Một cách chứng minh khác của bất đẳng thức tam giác:
Cho tam giác ABC. Giả sử BC là cạnh lớn nhất. kẻ đường vuông góc AH đến đường thẳng BC (H ε BC)
a) Dùng nhận xét về cạnh lớn nhất trong tam giác vuông để chứng minh AB + AC > BC
b) Từ giả thiết về cạnh BC, hãy suy ra hai bất đẳng thức tam giác còn lại
Cho tam giác ABC. Giả sử BC là cạnh lớn nhất. kẻ đường vuông góc AH đến đường thẳng BC (H ε BC)
a) Dùng nhận xét về cạnh lớn nhất trong tam giác vuông để chứng minh AB + AC > BC
b) Từ giả thiết về cạnh BC, hãy suy ra hai bất đẳng thức tam giác còn lại
Một cách chứng minh khác của bất đẳng thức tam giác:
Cho tam giác ABC. Giả sử BC là cạnh lớn nhất. Kẻ đường vuông góc AH đến đường thẳng BC (H thuộc BC).
Dùng nhận xét về cạnh lớn nhất trong tam giác vuông ở Bài 1 để chứng minh AB + AC > BC.
Một cách chứng minh khác của BĐT tam giác:
Cho ΔABC. Giả sử BC là cạnh lớn nhất. kẻ đường vuông góc AH đến đường thẳng BC (H ε BC)
a) Dùng nhận xét về cạnh lớn nhất trong Δvuông để chứng minh AB + AC > BC
b) Từ giả thiết về cạnh BC, hãy suy ra hai BĐT Δcòn lại
Bài 1: Tam giác ABC cân tại A ( góc A > 90 độ). Hai đường cao BD và CE cắt nhau tại H. Tia AH cắt BC tai I
a) Chứng minh tam giác ABD = tam giác ACE
b) Chứng minh I là trung điểm của BC
c) Từ C kẻ đường thẳng d vuông góc với AC. d cắt đường thẳng AH tại F. Chứng minh CB là tia phân giác của góc FCH
d) Giả sử góc BAC = 60 độ, AB = 4cm. Tính khoảng cách từ B đến đường thẳng CF
Bài 2: Tam giác ABC vuông tại A có AB = 9cm, AC = 12cm. Trên cạnh BC lấy điểm D sao cho BD = BA. Kẻ đường thẳng qua D vuông góc với BC, đường thẳng này cắt AC ở E và cắt AB ở K
a) Tính độ dài cạnh BC
b) Chứng minh tam giác ABE = tam giác DBE. Suy ra BE là tia phân giác góc ABC
c) Chứng minh AC = DK
d) Kẻ đường thẳng qua A vuông góc với BC tại H. Đường thẳng này cắt BE tại M. Chứng minh tam giác AME cân
Các bạn làm hộ mình nha, mình cần gấp lắm
Cho tam giác ABC vuông tại A có AB < AC .Kẻ AH vuông góc với BC ,AD là phân giác của góc HAC (D thuộc cạnh BC ). từ D kẻ DE vuông góc với AC. Đường thẳng AH cắt đường thẳng ED tại M
a)chứng minh tam giác AHD = tam giác AED rồi suy ra BH = DE
b) Chứng minh tam giác BMC cân
cho tam giác ABC vuông tại A, Có góc ABC = \(60^0\). Vẽ AH\(\perp\)BC (H thuộc BC ).
Phân giác của góc HAC cắt BC tại M. MN\(\perp\)AC (N thuộc AC)
a) giả sử AB=3cm, BC=5cm. Tính cạnh AC
b) chứng minh AM là đường trung trực của HN
c) chứng minh tam giác AHN là một tam giác đều
d) đường thẳng HN cắt AB ở D. chứng minh H là trung điểm của ND
Bài 1: Cho AABC = AEFG. Viết các cạnh bằng nhau và các góc bằng nhau. Hãy viết đẳng thức dưới một vài dạng khác. Giả sử A= 55° F=75° ; AB = 4cm; BC = Scm; EG = 7cm. Tính các gốc còn lại và chu vi của hai tam giác.
Bài 2: Cho biết A ABC = AMNP = ARST. a) Nếu A ABC vuông tại A thì các tam giác còn lại có vuông không? Vì sao? b) Cho biết thêm A =90°,S== 60°, Tính các góc còn lại của ba tam giác. c) Biết AB = 7cm, NP = 5cm; RT = 6cm. Tính các cạnh còn lại của ba tam giác và tính tổng chu vi của ba tam giác.
Bài 3: Cho biết AM là đường trung trực của BC (M e BC; A BC). Chứng tỏ rằng ABM=ACM; MAB=MAC, AB= AC.
Bài 4: Cho AABC có A = 90". Trên cạnh BC lấy điểm E sao cho AB = BE. Tia phân giác của B cắt cạnh AC ở D. Chứng minh: AABD=AEBD ) Chứng minh: B là d Chứng minh AB// CD