Đồ thị hai hàm số y = 2 x 2 - x + 1 x - 1 và y = x - 1 cắt nhau tại hai điểm A, B. Tính độ dài đoạn thẳng AB
A. AB = 2
B. A B = 2
C. A B = 10
D. A B = 1 2
Cho hàm số y= 2+ x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = 2 - x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x - 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x + 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y= 2+ x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = 2 - x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x - 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x + 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
a) Vẽ đồ thị của hàm số sau y = 2x + 2 b) Cho hai hàm số y = (2k + 2) * x - 3 và y = (1 - 3k) * x + 2 Với giá trị nào của k thi đồ thị của hai hàm số là hai đường thẳng cắt nhau ?
b: Để hai đường cắt nhau thì 2k+2<>1-3k
=>5k<>-1
=>k<>-1/5
Cho hai hàm số f ( x ) = a x 4 + b x 3 + c x 2 + d x + e với a ≠ 0 và g(x)= p x 2 + q x - 3 c ó đồ thị như hình vẽ bên dưới. Đồ thị hàm số y=f(x) đi qua gốc tọa độ và cắt đồ thị hàm số y=g(x) tại bốn điểm có hoành độ lần lượt là -2;-1;1 và m. Tiếp tuyến của đồ thị hàm số y=f(x)-g(x) tại điểm có hoành độ x=-2 có hệ số góc bằng -15/2. Gọi (H) là hình phẳng giới hạn bởi đồ thị hai hàm số y=f(x) và y=g(x) (phần được tô đậm trong hình vẽ). Diện tích của hình (H) bằng

A. 1553 120
B. 1553 240
C. 1553 60
D. 1553 30
Vẽ đồ thị hàm số \(y = {x^2} - 4x + 3\) rồi so sánh đồ thị hàm số này với đồ thị hàm số trong Ví dụ 2z. Nếu nhận xét về hai đồ thị này.
Tham khảo:
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = f(x) = {x^2} - 4x + 3\) là một parabol (P1):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 4)}}{{2.1}} = 2;{y_S} = {2^2} - 4.2 + 3 = - 1.\)
+ Có trục đối xứng là đường thẳng \(x = 2\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay lên trên vì \(a = 1 > 0\)
+ Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).
Ta vẽ được đồ thị như hình dưới.
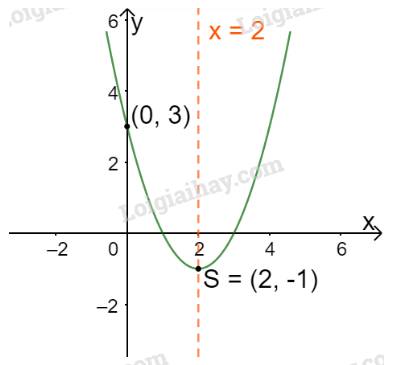
*So sánh với đồ thị hàm số ở Ví dụ 2a:
Giống nhau: Có chung trục đối xứng
Khác nhau:
Điểm đỉnh và giao điểm với trục tung của hai hàm số đối xứng với nhau qua trục Ox.
Bề lõm của (P) xuống dưới còn (P1) quay lên trên.
Nhận xét chung: Hai đồ thị này đối xứng với nhau qua trục Ox.
cho hai hàm số \(y=x^2\) và \(y=x+2\)
a, vẽ đồ thị của hai hàm số này tren cùng một hệ trục Oxy
b, tìm toạ độ các giao điểm M, N của hai đồ thị trên bằng phép tính
a, bạn tự kẻ hình nha
b,Phương trình hoành độ giao điểm của 2 đồ thị
\(x^2=x+2\) hay \(x^2-x-2=0\)
Phương trình có nghiệm: \(x_1=-1\Rightarrow y_1=1\) và \(x_2=2\Rightarrow y_2=4\)
Vậy 2 đồ thị cắt nhau tại 2 điểm \(M\left(-1;1\right)\) và \(N\left(2;4\right)\)
-Chúc bạn học tốt-
Bài 1 a) Khảo sát và vẽ đồ thị hàm số y=x³-2x²+x (C) b) từ đồ thị (C) suy ra đồ thị các hàm số sau: y=|x³-2x²+x|, y=|x|³ -2x²+|x| Bài 2: Khảo sát và vẽ đồ thị hàm số y=x⁴-2x²-3 (C). Từ đồ thị (C) suy ra đồ thị hàm số y=|y=x⁴-2x²-3|
Bài 1: Cho hàm số y=ax^2
a) Xác định a biết đồ thị của hàm số đi qua A(3;3)
b) Vẽ đồ thị hàm số vừa tìm được ở câu a
c) Tìm điểm thuộc đồ thị có tung độ bằng 1
Bài 2: Cho hai hàm số: y=x^2 (P) và y=2x (d)
a) vẽ đồ thị (P) và (d) của hai hàm số trên cùng một hệ trục tọa độ
b) Tìm tọa độ gioa điểm của (P) và (d)
Bài 3: Cho hai hàm số y= (m+1)x^2 và y= 2x-1.
Tìm m biết rằng đồ thị của hai hàm số cắt nhau tại điểm có hoành độ bằng 2
Cho hai hàm số y = x^2 và y =- x + 2.
a) Vẽ đồ thị của hai hàm số trên cùng một mặt phẳng tọa độ
b) Tìm tọa độ giao điểm của hai đồ thị trên bằng phương pháp đại số
c) Gọi A, B là giao điểm của 2 đồ thị trên. Tính diện tích tam giác AOB
Trên cùng một hệ trục tọa độ có hai đồ thị hàm số: (d1):y=-2x+5 và (d2):y=x+2
Biết hai đồ thị hàm số cắt nhau tại A. Tung độ giao điểm của hai đồ thị hàm số là