Giải phương trình y = s i n 6 x + c o s 6 x = 4 c o s 2 2 x . Nghiệm của phương trình là
A. y = a r c cos - 11 3 + k π 2
B. y = ± 1 4 a r c cos - 11 3 + k π 2
C. y = ± 1 4 a r c cos - 5 13 + k π 2
D. y = ± 1 4 a r c cos 1 3 + k π 2
Những câu hỏi liên quan
\(\text{Chứng minh phương trình sau luôn có nghiệm: a c o s 2 x + b s i n x + c o s x = 0}\)
\(\text{Đặt f (x)= a.cos2x+b.sinx+cosx}\)
\(\text{Hàm f (x) xác định và liên tục trên R}\)
\(\text{f ( π /4 ) = b √2 /2 + √2 /2 }\)
\(\text{f ( 5/π4 ) = − b √ 2/ 2 − √ 2/ 2 }\)
\(\text{⇒ f (π /4) . f ( 5 π/ 4 ) = − 1/2 ( b + 1 )^ 2 ≤ 0 ; ∀ a ; b ; c}\)
\(⇒ f (x)= 0 luôn có ít nhất 1 nghiệm thuộc đoạn [ π /4 ; 5π/4]\)
Hay pt đã có nghiệm.
Đúng 4
Bình luận (0)
Tập nghiệm của phương trình |2x| = x + 6 là: A. S = {-2; -6}. B. S = {2;6}. C. S = {-2;6}. D. S = { 2; -6}
|2x|=x+6
TH1: x>=0
=>2x=x+6
=>x=6(nhận)
TH2: x<0
=>-2x=x+6
=>-3x=6
=>x=-2(nhận)
Đúng 1
Bình luận (0)
Giải phương trình: \(\dfrac{1}{\text{x^2-3x+2}}+\dfrac{1}{\text{x^2-5x+6}}+\dfrac{1}{\text{x^2-7x+12}}+\dfrac{1}{\text{x^2-9x+20}}=\dfrac{1}{15}\) có tập nghiệm là:
A. S={-1;5} B. S={11} C. S=\(\varnothing\) D. S={11;-5}
\(đkxđ:x\ne1;2;3;4;5\\ \Leftrightarrow\dfrac{1}{\left(x-1\right)\left(x-2\right)}+\dfrac{1}{\left(x-2\right)\left(x-3\right)}+\dfrac{1}{\left(x-3\right)\left(x-4\right)}+\dfrac{1}{\left(x-4\right)\left(x-5\right)}=\dfrac{1}{15}\\ \Leftrightarrow-\dfrac{1}{x-1}+\dfrac{1}{x-2}-\dfrac{1}{x-2}+\dfrac{1}{x-3}-\dfrac{1}{x-3}+\dfrac{1}{x-4}-\dfrac{1}{x-4}+\dfrac{1}{x-5}=\dfrac{1}{15}\\ \Leftrightarrow\dfrac{1}{x-5}-\dfrac{1}{x-1}=\dfrac{1}{15}\\ \Leftrightarrow60=x^2-6x+5\\ \)
\(\Leftrightarrow60=x^2-6x+5\\ \Leftrightarrow\left[{}\begin{matrix}x-11=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=11\\x=-5\end{matrix}\right.\\ \Rightarrow D\)
Đúng 2
Bình luận (0)
Trong không gian Oxyz, cho điểm A(1;0;-1), mặt phẳng (P): x + y - z - 3 0. Mặt cầu (S) có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác OIA bằng 6 + √2. Phương trình mặt cầu (S) là: A. (x + 2)2 + (y - 2)2 + (z + 1)2 9 và (x + 1)2 + (y - 2)2 + (z + 2)2 9 B. (x - 2)2 + (y - 2)2 + (z - 1)2 9 và x2 + y2 + (z + 3)2 9 C. (x + 2)2 + (y - 2)2 + (z + 1)2 9 và (x + 1)2 + (y - 2)2 + (z + 2)2 9 D. (x + 1)2 + (y - 2)2 + (z + 2)2 9 và (x - 2)...
Đọc tiếp
Trong không gian Oxyz, cho điểm A(1;0;-1), mặt phẳng (P): x + y - z - 3 = 0. Mặt cầu (S) có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác OIA bằng 6 + √2. Phương trình mặt cầu (S) là:
A. (x + 2)2 + (y - 2)2 + (z + 1)2 = 9 và (x + 1)2 + (y - 2)2 + (z + 2)2 = 9
B. (x - 2)2 + (y - 2)2 + (z - 1)2 = 9 và x2 + y2 + (z + 3)2 = 9
C. (x + 2)2 + (y - 2)2 + (z + 1)2 = 9 và (x + 1)2 + (y - 2)2 + (z + 2)2 = 9
D. (x + 1)2 + (y - 2)2 + (z + 2)2 = 9 và (x - 2)2 + (y - 2)2 + (z - 1)2 = 9
Chọn D
Giả sử (S): x2 + y2 + z2 - 2ax - 2by - 2cz + d = 0 (a2 + b2 + c2 - d > 0)
và tâm I (a;b;c) ∈ (P) => a + b - c - 3 = 0 (1)
(S) qua A và O nên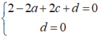 
Cộng vế theo vế (1) và (2) ta suy ra b = 2. Từ đó, suy ra I (a; 2; a-1)
Chu vi tam giác OAI bằng 6 + √2 nên OI + OA + AI = 6 + √2
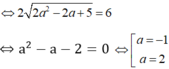
+ Với a = -1 => A (-1; 2; -2) => R = 3. Do đó:
+ Với a = 2 => I (2;2;1) => R = 3. Do đó:
Đúng 0
Bình luận (0)
Cho đường thẳng
d
:
x
+
5
2
y
-
7
-
2
z
1
và điểm
I
(
4
;
1
;
6
)
.
Đường thẳng d cắt mặt cầu (S) có tâm I, tại hai điểm A, B sao cho
A
B
...
Đọc tiếp
Cho đường thẳng d : x + 5 2 = y - 7 - 2 = z 1 và điểm I ( 4 ; 1 ; 6 ) . Đường thẳng d cắt mặt cầu (S) có tâm I, tại hai điểm A, B sao cho A B = 6 . Phương trình của mặt cầu (S) là:
A. x - 4 2 + y - 1 2 + z - 6 2 = 18
B. x + 4 2 + y + 1 2 + z + 6 2 = 18
C. x - 4 2 + y - 1 2 + z - 6 2 = 9
D. x - 4 2 + y - 1 2 + z - 6 2 = 16
Chọn A
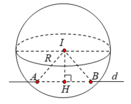
Đường thẳng d đi qua M(-5;7;0) và có vectơ chỉ phương 
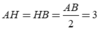
Gọi H là hình chiếu của I lên (d). Ta có:
Đúng 0
Bình luận (0)
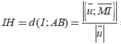
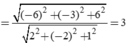
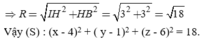
phương trình truyền sóng trên dây dài là u=4cos(2pit-0.5pix) cm trong đó t tính bằng s và x tính bằng cm . Một điểm trên dây có x=5/6 cm vào lúc t=1/3 s có li độ là :
A . 0,98 cm
B . 2,45 cm
C . 3.50 cm
D . 2.83 cm (*)
Gọi là tập hợp gồm các giá trị thực của tham số m để phương trình \(x-2\sqrt{x+2}-m-3=0\) có 2 nghiệm phân biệt . Mệnh đề đúng là :
\(A,S=\left(-6;-5\right)\)
\(B,S=(-6;-5]\)
\(C,S=[-6;-5)\)
\(D,S=\left(-6;+\infty\right)\)
Lời giải:
Đặt $\sqrt{x+2}=t(t\geq 0)$ thì pt trở thành:
$t^2-2-2t-m-3=0$
$\Leftrightarrow t^2-2t-(m+5)=0(*)$
Để PT ban đầu có 2 nghiệm pb thì PT $(*)$ có 2 nghiệm không âm phân biệt.
Điều này xảy ra khi \(\left\{\begin{matrix} \Delta'=1+m+5>0\\ S=2>0\\ P=-(m+5)\geq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m>-6\\ m\leq -5\end{matrix}\right.\)
Đáp án B.
Đúng 2
Bình luận (0)
giải phương trình
\(\frac{x^2+2x+1}{x^2+2x+2}+\frac{x^2+2x+2}{x^2+2x+3}\)= \(\frac{7}{6}\)
Giải SBT Vật Lí 6 Bài 11: Khối lượng riêng - Trọng lượng riêng
Để học tốt Vật Lí lớp 6, dưới đây liệt kê các bài giải bài tập Sách bài tập Vật Lí 6 Bài 11: Khối lượng riêng - Trọng lượng riêng. Bạn vào tên bài hoặc Xem lời giảiđể theo dõi bài giải sbt Vật Lí 6 tương ứng.
Bài 11.1 (trang 38 Sách bài tập Vật Lí 6): Muốn đo khối lượng riêng của các hòn bi ...
Xem lời giải
Bài 11.2 (trang 38 Sách bài tập Vật Lí 6): Một hộp sữa Ông Thọ có khối lượng 397g ...
Xem lời giải
Bài 11...
Đọc tiếp
Giải SBT Vật Lí 6 Bài 11: Khối lượng riêng - Trọng lượng riêng
Để học tốt Vật Lí lớp 6, dưới đây liệt kê các bài giải bài tập Sách bài tập Vật Lí 6 Bài 11: Khối lượng riêng - Trọng lượng riêng. Bạn vào tên bài hoặc Xem lời giảiđể theo dõi bài giải sbt Vật Lí 6 tương ứng.
Bài 11.1 (trang 38 Sách bài tập Vật Lí 6): Muốn đo khối lượng riêng của các hòn bi ...
Xem lời giải
Bài 11.2 (trang 38 Sách bài tập Vật Lí 6): Một hộp sữa Ông Thọ có khối lượng 397g ...
Xem lời giải
Bài 11.3 (trang 38 Sách bài tập Vật Lí 6): Biết 10 lít cát có khối lượng 15kg ...
Xem lời giải
Bài 11.4 (trang 38 Sách bài tập Vật Lí 6): 1kg kem giặt VISO có thể tích 900cm3. ...
Xem lời giải
Bài 11.5 (trang 38 Sách bài tập Vật Lí 6): Một hòn gạch "hai lỗ" có khối lượng 1,6kg. ...
Xem lời giải
Bài 11.6 (trang 38 Sách bài tập Vật Lí 6): Hãy tìm cách đo khối lượng riêng của cát khô ...
Xem lời giải
Bài 11.7 (trang 38 Sách bài tập Vật Lí 6): Khối lượng riêng của nhôm là bao nhiêu? ...
Xem lời giải
Bài 11.8 (trang 38 Sách bài tập Vật Lí 6): Trọng lượng riêng của gạo vào khoảng? ...
Xem lời giải
Bài 11.9 (trang 38 Sách bài tập Vật Lí 6): Khối lượng riêng của sắt là 7800kg/m3. ...
Xem lời giải
Bài 11.10 (trang 39 Sách bài tập Vật Lí 6): Khối lượng riêng của dầu ăn vào khoảng ...
Xem lời giải
Bài 11.11 (trang 39 Sách bài tập Vật Lí 6): Người ta nói đồng nặng hơn nhôm. ...
Xem lời giải
Bài 11.12 (trang 39 Sách bài tập Vật Lí 6): Cho biết 1kg nước có thể có thể tích 1 lít ...
Xem lời giải
Bài 11.13 (trang 39 Sách bài tập Vật Lí 6): Một học sinh định xác định khối lượng riêng D ...
Xem lời giải
Bài 11.14 (trang 40 Sách bài tập Vật Lí 6): Trong phòng thí nghiệm người ta xác định ...
Xem lời giải
Bài 11.15 (trang 40 Sách bài tập Vật Lí 6): Trò chơi ô chữ ...
Xem lời giải
giải phương trình nghiệm nguyên 4^x+5^y=6^z với x;y;z thuộc N
Theo đề: \(5^y=6^z-4^x\)
Vì \(y\inℕ\)nên vế trái chắc chắn là số lẻ do đó vế phải cũng lẻ
Mà \(6^z,4^x\)đều là lũy thừa cơ số chẵn do vậy 1 trong 2 \(x,z\)phải bằng \(0\)
Mà \(6^z-4^x=5^y>0\Rightarrow6^z>4^x\)nên \(z\)không thể bằng \(0\)
Do đó \(x=0\)
\(\Rightarrow6^z-5^y=1\)vì các lũy thừa bậc cao của 5 và 6 không thể là các số tự nhiên liên tiếp nên \(y=z=1\)
Vậy nghiệm của phương trình là \(x=0,y=z=1\)