Cho tứ diện OABC có các góc tại đỉnh O đều bằng 90 ° và O A = a , O B = b ; O C = c . Gọi G là trọng tâm của tứ diện. Thể tích của khối tứ diện GABC bằng
A. a b c 6
B. a b c 8
C. a b c 4
D. a b c 24
Trong không gian với hệ tọa độ Oxy, cho mặt phẳng (P): 2y-z+3=0 và điểm A (2;0;0). Mặt phẳng (α) đi qua A, vuông góc với (P), cách gốc tọa độ O một khoảng bằng 4/3 và cắt các tia Oy, Oz lần lượt tại các điểm B, C khác O. Thể tích khối tứ diện OABC bằng:
A. 8.
B. 16
C. 8/3
D. 16/3
Chọn C
Giả sử B (0;b;0) và C (0;0;c), với b, c > 0.
Khi đó phương trình mặt phẳng (α) là: ![]()
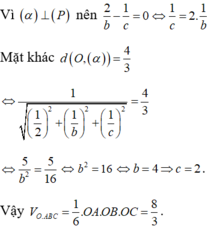
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):2y-z+3=0 và điểm A(2;0;0). Mặt phẳng (α) đi qua A, vuông góc với (P), cách gốc tọa độ O một khoảng bằng 4/3 và cắt các tia Oy,Oz lần lượt tại các điểm B,C khác O. Thể tích khối tứ diện OABC bằng
A. 8.
B. 16.
C. 8/3
D. 16/3
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng ( P ) : 2 y - z + 3 = 0 và điểm A(2;0;0). Mặt phẳng ( α ) đi qua A, vuông góc với (P), cách gốc tọa độ O một khoảng bằng 4 3 và cắt các tia Oy, Oz lần lượt tại các điểm B, C khác O. Thể tích khối tứ diện OABC bằng:
A. 8.
B. 16.
C. 8 3
D. 16 3
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : 2 y − z + 3 = 0 và điểm A 2 ; 0 ; 0 .
Mặt phẳng α đi qua A, vuông góc với P , cách gốc tọa độ O một khoảng bằng 4 3 và cắt các tia Oy, Oz lần lượt tại các điểm B, C khác O. Thể tích khối tứ diện OABC bằng
A. 8
B. 16
C. 8 3 .
D. 16 3 .
Đáp án C.
Phương pháp:
- Viết phương trình mặt phẳng α .
- Tìm tọa độ giao điểm B, C của α với trục Oy, Oz.
- Tính thể tích khối tứ diện vuông OABC: V = 1 6 . O A . O B . O C .
Cách giải:
Giả sử n → a ; b ; c , a 2 + b 2 + c 2 ≠ 0 là một vecto pháp tuyến của (P).
Vì α đi qua A 2 ; 0 ; 0 nên PTTQ của (P):
a x − 2 + b y − 0 + c z − 0 = 0
⇔ a x + b y + c z − 2 a = 0.
Vì α vuông góc với α nên n → a ; b ; c vuông góc với n 1 → 0 ; 2 ; − 1 .
Khi đó,
0. a + 2. b + − 1 . c = 0 ⇔ c = 2 b
⇒ α : a x + b y + 2 b z − 2 a = 0
d O ; α = 4 3 ⇔ − 2 a a 2 + b 2 + 4 b 2 = 4 3 ⇔ 6 a 2 = 16 a 2 + 5 b 2 ⇔ a 2 = 4 b 2 ⇔ a = 2 b a = − 2 b
Cho
b = 1 ⇒ a = 2 a = − 2 ⇒ n → 2 ; 1 ; 2 n → − 2 ; 1 ; 2 ⇒ α : 2 x + y + 2 z − 4 = 0 α : − 2 x + y + 2 z + 4 = 0
+ ) α : 2 x + y + 2 z − 4 = 0 ⇒ B 0 ; 4 ; 0 , C 0 ; 0 ; 2 ⇒ V O A B C = 1 6 . 2 . 4 . 2 = 8 3
+ ) α : − 2 x + y + 2 z + 4 = 0 ⇒ B 0 ; − 4 ; 0 , C 0 ; 0 ; − 2 ⇒ V O A B C = 1 6 . 2 . − 4 . − 2 = 8 3
Vậy thể tích khối tứ diện OABC là 8 3 .
Trong không gian cho ba tia Ox,Oy,Oz đôi một vuông góc và các điểm A,B,C không trùng với O lần lượt thay đổi trên các tia Ox,Oy,Oz và luôn thoả mãn điều kiện: tỉ số giữa diện tích tam giác ABC và thể tích khối tứ diện OABC bằng 3 2 Khối diện OABC có thể tích nhỏ nhất bằng
![]()
![]()
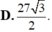
Trong không gian cho ba tia Ox,Oy,Oz đôi một vuông góc và các điểm A,B,C không trùng với O lần lượt thay đổi trên các tia Ox,Oy,Oz và luôn thoả mãn điều kiện: tỉ số giữa diện tích tam giác ABC và thể tích khối tứ diện OABC bằng 3 2 . Khối diện OABC có thể tích nhỏ nhất bằng
A. 6
B. 3 2
C. 4 3
D. 27 3 2
cho đường tròn tâm O,bán kính OB,H là trung điểm của OB.Dây AC vuông góc OB tại H
a) tứ giác OABC là hình gì
b) qua A và C vẽ các tiếp tuyến với đường tròn tâm O,hai tiếp tuyến này cắt nhau tại N . Chứng minh rằng tam giác NAC đều
c) chứng minh rằng N,B,O thẳng hàng bằng hai cách
Cho tứ giác ABCD có góc A bằng góc B bằng 90o và góc B bằng 150o góc C bằng 30o. M là trung điểm của BD. CM tam giác AMC đều.
ủa tự nhiên tứ giác abcd có góc b =90 độ mà còn và góc b bằng 150 độ nx là sao
một là ông ghi kí tự của tứ giác bị sai hoặc là ông ghi để sai
Cho tứ diện vuông OABC đỉnh O. Biết OA=2OB=3OC=6a, tính chiều cao kẻ từ đỉnh O của tứ diện OABC.
Trong tam giác OBC, kẻ đường cao OH \(\Rightarrow BC\perp\left(AOH\right)\)
\(\frac{1}{OH^2}=\frac{1}{OB^2}+\frac{1}{OC^2}\Rightarrow OH=\frac{OB.OC}{\sqrt{OB^2+OC^2}}=\frac{6a}{\sqrt{13}}\)
Trong tam giác vuông AOH, từ O kẻ \(OK\perp AH\Rightarrow OK\perp\left(ABC\right)\)
\(\frac{1}{OK^2}=\frac{1}{OH^2}+\frac{1}{OA^2}\Rightarrow OK=\frac{OA.OH}{\sqrt{OA^2+OH^2}}=\frac{3a\sqrt{14}}{7}\)