Tìm số giao điểm của đồ thị hàm số y = x - 1 x 2 - 2 x với trục hoành.
A. 1
B. 2
C. 0
D. 3
tìm toạ độ giao điểm của đồ thị hàm số y = 4x và đồ thị hàm số y=1/x
Tọa độ giao điểm của đồ thị hàm số \(y=4x\) và y=\(\frac{1}{x}\) là các giá trị x\(\in\) \(Z\) sao cho:
\(4x=\frac{1}{x}\)
\(4x^2=1\)
\(x^2=\frac{1}{4}\)
\(x=\) \(\pm\) \(\sqrt{\frac{1}{2}}\)
\(\implies\) \(\orbr{\begin{cases}x=\frac{1}{2}\\x=-\frac{1}{2}\end{cases}}\) \(\implies\) \(\orbr{\begin{cases}y=4.\frac{1}{2}=2\\y=4.\left(-\frac{1}{2}\right)=-2\end{cases}}\)
\(\implies\) Đồ thị hàm số \(y=4x\) cắt đồ thị hàm số \(y=\frac{1}{x}\) tại \(2\) giao điểm \(\left(\frac{1}{2};2\right),\left(-\frac{1}{2};-2\right)\)
Tọa độ giao điểm của hai đồ thị phải thỏa mãn đồng thời cả hai hàm số
tức là \(\hept{\begin{cases}y=4x\\y=\frac{1}{x}\end{cases}}\)Suy ra \(4x=\frac{1}{x}\Rightarrow4x^2=1\Rightarrow\orbr{\begin{cases}x=\frac{1}{2}\\x=\frac{-1}{2}\end{cases}}\)
Với \(x=\frac{1}{2}\Rightarrow y=\frac{1}{2}.4=2\)
Với \(x=\frac{-1}{2}\Rightarrow y=\frac{-1}{2}.4=-2\)
Vậy hai đồ thị có hai giao điểm là \(M\left(\frac{1}{2};2\right)\)và \(N\left(\frac{-1}{2};-2\right)\)
Chúc các em học tốt!
Cho hàm số bậc nhất y=x+2 (d)
a) vẽ đồ thị hàm số trên
b) tìm tọa độ giao điểm của hàm số (d) với đồ thị của hàm số y=2x-1
b: Tọa độ giao điểm là:
2x-1=x+2 và y=x+2
=>3x=3 và y=x+2
=>x=1 và y=3
a: 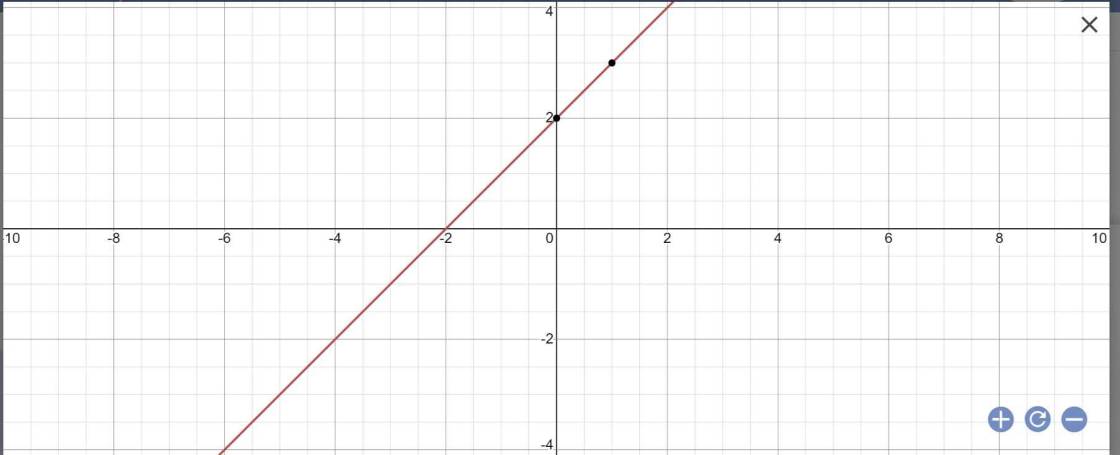
cho hàm số y=-2x+1a)Xác định tọa độ giao điểm của đồ thị hàm số trên và Ox,Oy
b)CMR:f(x1)+f(x2)=f(x1+x2)+1
c)Tìm tọa độ giao điểm của đồ thị hàm số trên và đồ thị hàm số y=|x|
a) Tọa độ giao điểm của đồ thị hàm số y=-2x+1 với trục Ox là nghiệm của hệ phương trình:
\(\left\{{}\begin{matrix}y=-2x+1\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2x+1=0\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2x=-1\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=0\end{matrix}\right.\)
Tọa độ giao điểm của đồ thị hàm số y=-2x+1 với trục Oy là nghiệm của hệ phương trình:
\(\left\{{}\begin{matrix}x=0\\y=-2x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=-2\cdot0+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\)
Tìm số giao điểm của đồ thị hàm số y = x/(x + 1) và đường thẳng y = -x.
A. 3
B. 1
C. 2.
D. 0
Đáp án C.
Phương trình hoành độ giao điểm x/(x + 1) = -x (DK: x ≠ -1)
⇔ x = -x2 – x
⇔ x2 + 2x = 0
⇔ ![]()
Tìm số giao điểm của đồ thị hai hàm số y = x + 3 và y = x + 1.
A. 2
B. 3
C. 1
D. 0
Đáp án C
PT hoành độ giao điểm là:
x + 3 = x + 1 ⇔ x + 1 ≥ 0 x + 3 = x + 1 2 ⇔ x ≥ − 1 x 2 + x − 2 = 0 ⇔ x ≥ − 1 x = 1 x = − 2 ⇒ x = 1.
Cho hàm số y=(1-2m)x+3 a) tìm m biết đồ thị hàm số đi qua điểm A(1;0) b) tìm m biết đồ thị hàm số đi qua điểm B(2;-4) c) tìm toạ độ giao điểm của 2 đồ thị hàm số ở câu a,b
a: Thay x=1 và y=0 vào (d), ta được:
1-2m+3=0
\(\Leftrightarrow m=2\)
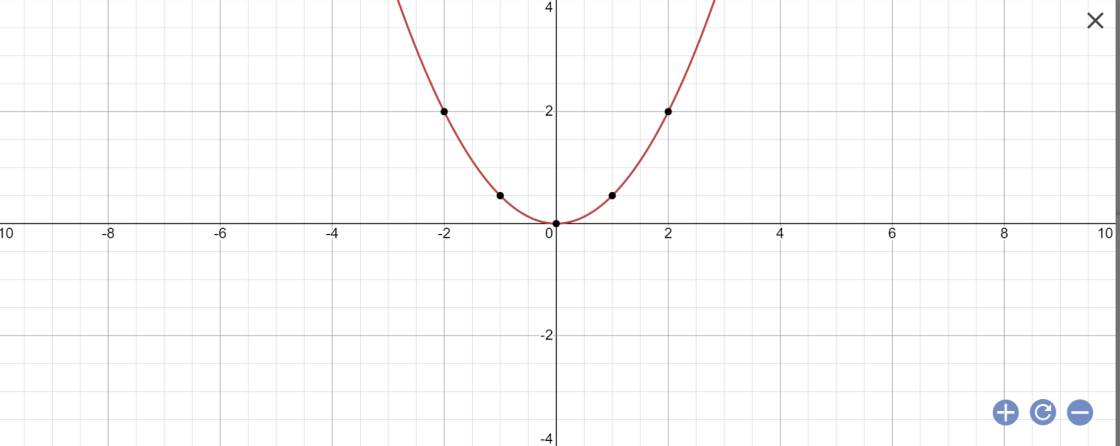
Cho hai hàm số y=1/4 x² và y=x-1
a) biểu diễn đồ thị của hai hàm số trên cùng một mặt phẳng tọa độ
b) tìm tọa độ giao điểm của hai đồ thị
\(a,y=\dfrac{1}{4}x^2\)
Cho \(x=1=>y=\dfrac{1}{4}\\ x=2=>y=1\\ x=3=>y=\dfrac{9}{4}\\ x=4=>y=4\\ x=5=>y=\dfrac{25}{4}\)
Vẽ đồ thị đi qua các điểm \(\left(1;\dfrac{1}{4}\right);\left(2;1\right);\left(3;\dfrac{9}{4}\right);\left(4;4\right);\left(2;\dfrac{25}{4}\right)\)
\(y=x-1\)
\(Cho\) \(x=0=>y=-1\) ta được điểm \(\left(0;-1\right)\)
Cho \(y=0=>x=1\) ta được điểm \(\left(1;0\right)\)
Vẽ đồ thị đi qua hai điểm \(\left(0;-1\right);\left(1;0\right)\)
b, Hoành độ giao điểm của hai hàm số là nghiệm của pt
\(\dfrac{1}{4}x^2=x-1\\ < =>\dfrac{1}{4}x^2-x+1=0\\ < =>x=2\)
Thay \(x=2\) vào \(y=x-1\)
\(\Leftrightarrow y=2-1=1\)
Vậy tọa độ giao điểm là \(\left(2;1\right)\)
Lời giải:
a. Bạn có thể tự vẽ
b. PT hoành độ giao điểm: $\frac{1}{4}x^2=x-1$
$\Leftrightarrow x^2=4(x-1)$
$\Leftrightarrow x^2-4x+4=0$
$\Leftrightarrow (x-2)^2=0\Leftrightarrow x=2$
Với $x=2$ thì $y=x-1=2-1=1$
Vậy tọa độ giao điểm của 2 đths là $(2,1)$
Bài 1 : Cho hàm số bậc nhất y=(2m-1)x +3m
a. Tìm m để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2
b. Tìm m để đô thị hàm số song song với đường thẳng y = x-1
c. Tìm m để đồ thị hàm số đi qua giao điểm của 2 đường thẳng sau : y= 3x+2-4
d. Tìm m để đô thị hàm số cắt đường thẳng y= 2x+1 tại điểm có hoành độ là -4
e. Tìm m để đô thị hàm số cắt đường thẳng y=3x-5 tại điểm có tung độ là 2
Cho hàm số y = ax2a) Xác định a để đồ thị của hàm số trên đi qua điểm A (4 ; 4).
b) Vẽ đồ thị của hàm số trên với a vừa tìm được và đồ thị của hàm số y = \(-\dfrac{1}{2}x\) trên cùng một mặt phẳng tọa độ Oxy.
c) Tìm tọa độ giao điểm của hai hàm số trên (câu b) bằng phép toán.
a) Để đồ thị hàm số \(y=ax^2\) đi qua điểm A(4;4) thì
Thay x=4 và y=4 vào hàm số \(y=ax^2\), ta được:
\(a\cdot4^2=4\)
\(\Leftrightarrow a\cdot16=4\)
hay \(a=\dfrac{1}{4}\)
a, - Thay tọa độ điểm A vào hàm số ta được : \(4^2.a=4\)
\(\Rightarrow a=\dfrac{1}{4}\)
b, Thay a vào hàm số ta được : \(y=\dfrac{1}{4}x^2\)
- Ta có đồ thì của hai hàm số :
c, - Xét phương trình hoành độ giao điểm :\(\dfrac{1}{4}x^2=-\dfrac{1}{2}x\)
\(\Leftrightarrow x^2+2x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
Vậy hai hàm số trên cắt nhau tại hai điểm : \(\left(0;0\right);\left(-2;1\right)\)
Cho hàm số y=1/2 x^2 có đồ thị là (P) a) Vẽ đồ thị (P) của hàm số trên b) Tìm toạ độ giao điểm của (P) và đường thẳng (d) : y = x + 4
b: PTHĐGĐ là:
1/2x^2-x-4=0
=>x^2-2x-8=0
=>(x-4)(x+2)=0
=>x=4 hoặc x=-2
=>y=8 hoặc y=2
a: