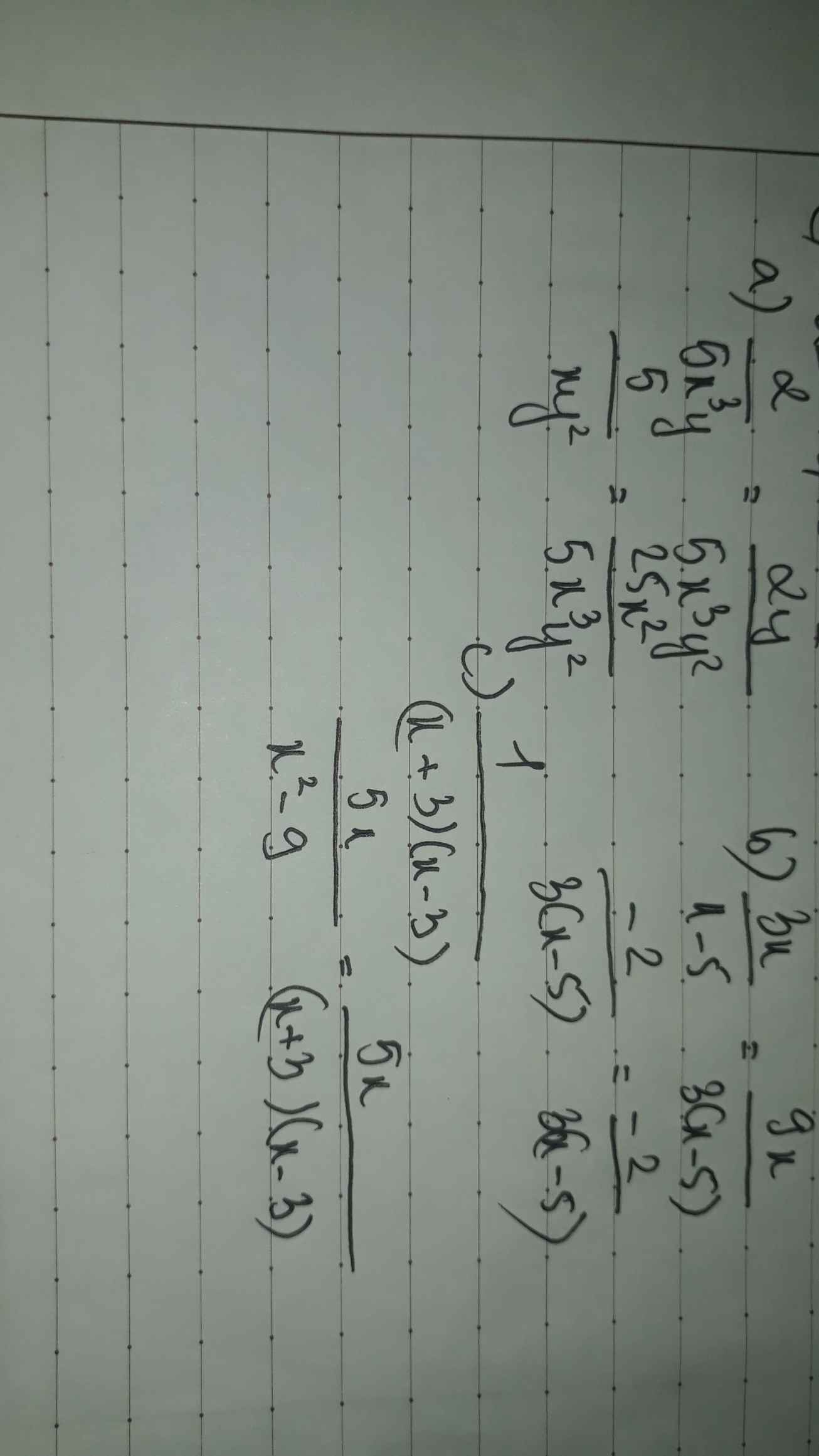\(\dfrac{3}{5}x^3y\left(10xy^3-\dfrac{5}{3}y^2+\dfrac{5}{6}xy\right)\) help em vs mn ơi

Những câu hỏi liên quan
Sos mn ơi
Tìm Y
\(\dfrac{11}{4}-y-\dfrac{2}{5}=\dfrac{1}{3}\). \(\dfrac{5}{3}x\left(\dfrac{3}{4}-y:\dfrac{2}{5}\right)=\dfrac{5}{8}\)
\(\dfrac{3}{2}xy-\dfrac{3}{4}xy+y=\dfrac{4}{5}\)
Câu đầu em xem lại đề bài sao có hai dấu bằng.
Câu 2:
\(\dfrac{3}{2}\) \(\times\)y - \(\dfrac{3}{4}\) \(\times\)y + y = \(\dfrac{4}{5}\)
y \(\times\) ( \(\dfrac{3}{2}\) - \(\dfrac{3}{4}\) + 1) = \(\dfrac{4}{5}\)
y \(\times\) (\(\dfrac{6}{4}\) - \(\dfrac{3}{4}\) + \(\dfrac{4}{4}\)) = \(\dfrac{4}{5}\)
y \(\times\) \(\dfrac{7}{4}\) = \(\dfrac{4}{5}\)
y = \(\dfrac{4}{5}\): \(\dfrac{7}{4}\)
y = \(\dfrac{16}{35}\)
Đúng 2
Bình luận (0)
Rút gọn các phân thức sau:
a) \(\dfrac{6x^2y^2}{8xy^{ }5}\)
b) \(\dfrac{10xy^2\left(x+y\right)}{15xy\left(x+y\right)^3}\)
c) \(\dfrac{2x^2+2x
}{x+1}\)
d) \(\dfrac{x^2-xy-x+y}{x^2+xy-x-y}\)
e) \(\dfrac{36\left(x-2\right)^3}{32-16x}\)
a) \(\dfrac{6x^2y^2}{8xy^5}=\dfrac{3x}{4y^3}\)
b) \(=\dfrac{2y}{3\left(x+y\right)^2}=\dfrac{2y}{3x^2+6xy+3y^2}\)
c) \(=\dfrac{2x\left(x+1\right)}{x+1}=2x\)
d) \(=\dfrac{x\left(x-y\right)-\left(x-y\right)}{x\left(x+y\right)-\left(x+y\right)}=\dfrac{\left(x-y\right)\left(x-1\right)}{\left(x+y\right)\left(x-1\right)}=\dfrac{x-y}{x+y}\)
e) \(=\dfrac{36\left(x-2\right)^3}{-16\left(x-2\right)}=-9\left(x-2\right)^2=-9x^2+36x-36\)
Đúng 1
Bình luận (0)
\(\dfrac{2x-5}{3}=\dfrac{x+2}{2}\) help em vs mn ơi
\(\left(2x-5\right).2=\left(x+2\right).3\)
\(\Rightarrow4x-10=3x+6\)
\(\Rightarrow x=16\)
Đúng 0
Bình luận (0)
\(\dfrac{2x+5}{3}=\dfrac{x+2}{2}\)
MTC : 6
Quy đồng mẫu thức :
\(\Rightarrow\) \(\dfrac{2\left(2x+5\right)}{6}=\)\(\dfrac{3\left(x+2\right)}{6}\)
Suy ra : 2(2x + 5) = 3(x + 2)
\(\Leftrightarrow\) 4x + 10 = 3x + 6
\(\Leftrightarrow\) 4x + 10 - 3x - 6 = 0
\(\Leftrightarrow\) x + 4 = 0
\(\Leftrightarrow\) x = - 4
Vậy S = \(\left\{-4\right\}\)
Chúc bạn học tốt
Đúng 1
Bình luận (3)
quy đồng mẫu thức của các phân tử
a, \(\dfrac{2}{5x^3y};\dfrac{5}{xy^2}\)
b, \(\dfrac{3x}{x-5};\dfrac{-2}{3\left(x-5\right)}\)
c, \(\dfrac{1}{\left(x+3\right)\left(x-3\right)};\dfrac{5x}{x^2-9}\)
BT10: Thực hiện phép tínha,-xyz^2-3xz.yzb,-8x^2y-x.left(xyright)c,4xy^2 .x-left(-12x^2y^2right)d,dfrac{1}{2}x^2y^3-dfrac{1}{3}x^2y.y^2e,3xyleft(x^2yright)-dfrac{5}{6}x^3y^2f,dfrac{3}{4}x^4y-dfrac{1}{6}xy.x^3
Đọc tiếp
BT10: Thực hiện phép tính
\(a,-xyz^2\)\(-3xz.yz\)
\(b,-8x^2\)\(y-x.\left(xy\right)\)
\(c,4xy^2\) \(.x-\left(-12x^2y^2\right)\)
\(d,\dfrac{1}{2}x^2y^3-\dfrac{1}{3}x^2y.y^2\)
\(e,3xy\left(x^2y\right)-\dfrac{5}{6}x^3y^2\)
\(f,\dfrac{3}{4}x^4y-\dfrac{1}{6}xy.x^3\)
a: =-4xyz^2
b: =-9x^2y
c: =16x^2y^2
d: =1/6x^2y^3
e: =13/6x^3y^2
f: =7/12x^4y
Đúng 1
Bình luận (0)
a) -xyz² - 3xz.yz
= -xyz² - 3xyz²
= -4xyz²
b) -8x²y - x.(xy)
= -8x²y - x²y
= -9x²y
c) 4xy².x - (-12x²y²)
= 4x²y² + 12x²y²
= 16x²y²
d) 1/2 x²y³ - 1/3 x²y.y²
= 1/2 x²y³ - 1/3 x²y³
= 1/6 x²y³
e) 3xy(x²y) - 5/6 x³y²
= 3x³y² - 5/6 x³y²
= 13/6 x³y²
f) 3/4 x⁴y - 1/6 xy.x³
= 3/4 x⁴y - 1/6 x⁴y
= 7/12 x⁴y
Đúng 1
Bình luận (0)
\(\left\{{}\begin{matrix}5y-5x=xy\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{4}{5}\\\end{matrix}\right.\)
\(\left\{{}\begin{matrix}\dfrac{1}{2x-3y}+\dfrac{5}{3x+y}=\dfrac{5}{8}\\\dfrac{3}{2x-3y}-\dfrac{5}{3x+y}=-\dfrac{3}{8}\\\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x-y=2\\y-3z=2\\-3x-2y+z=-2\end{matrix}\right.\)
a) \(\left\{{}\begin{matrix}5y-5x=xy\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{4}{5}\end{matrix}\right.\) \(\Leftrightarrow\)\(\left\{{}\begin{matrix}5y-5x=xy\\\dfrac{x+y}{xy}=\dfrac{4}{5}\end{matrix}\right.\)
\(\Leftrightarrow\)\(\left\{{}\begin{matrix}5y-5x=xy\\5\left(x+y\right)=4xy\end{matrix}\right.\)\(\Leftrightarrow\)\(\left\{{}\begin{matrix}5y-5x=xy\\5\left(x+y\right)=4\left(5y-5x\right)\end{matrix}\right.\)
\(\Leftrightarrow\)\(\left\{{}\begin{matrix}5y-5x=xy\\5x+5y=20y-20x\end{matrix}\right.\)\(\Leftrightarrow\)\(\left\{{}\begin{matrix}5y-5x=xy\\5x+5y-20y+20x=0\end{matrix}\right.\)
\(\Leftrightarrow\)\(\left\{{}\begin{matrix}5y-5x=xy\\-15y+25x=0\end{matrix}\right.\)\(\Leftrightarrow\)\(\left\{{}\begin{matrix}5y-5x=xy\\-5\left(3y-5x\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\)\(\left\{{}\begin{matrix}5y-5x=xy\\3y-5x=0\end{matrix}\right.\)\(\Leftrightarrow\)\(\left\{{}\begin{matrix}5y-5x=xy\\5x=3y\end{matrix}\right.\)\(\Leftrightarrow\)\(\left\{{}\begin{matrix}5y-3y=xy\\5x=3y\end{matrix}\right.\)
\(\Leftrightarrow\)\(\left\{{}\begin{matrix}2y=xy\\5x=3y\end{matrix}\right.\)\(\Leftrightarrow\)\(\left\{{}\begin{matrix}x=2\\y=\dfrac{10}{3}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
b) \(\left\{{}\begin{matrix}\dfrac{1}{2x-3y}+\dfrac{5}{3x+y}=\dfrac{5}{8}\\\dfrac{2}{2x-3y}-\dfrac{5}{3x+y}=\dfrac{-3}{8}\end{matrix}\right.\)
Đặt \(\dfrac{1}{2x-3y}=a;\dfrac{1}{3x+y}=b\)
=> hpt <=> \(\left\{{}\begin{matrix}a+5b=\dfrac{5}{8}\\2a-5b=\dfrac{-3}{8}\end{matrix}\right.\)
\(\Leftrightarrow\)\(\left\{{}\begin{matrix}a+5b=\dfrac{5}{8}\\2a-5b+a+5b=\dfrac{-3}{8}+\dfrac{5}{8}=0,25\end{matrix}\right.\)
\(\Leftrightarrow\)\(\left\{{}\begin{matrix}a+5b=\dfrac{5}{8}\\3a=0,25\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a+5b=\dfrac{5}{8}\\a=\dfrac{1}{12}\end{matrix}\right.\)
\(\Leftrightarrow\)\(\left\{{}\begin{matrix}a=\dfrac{1}{12}\\b=\dfrac{13}{120}\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{2x-3y}=\dfrac{1}{12}\\\dfrac{1}{3x+y}=\dfrac{13}{120}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-3y=12\\3x+y=\dfrac{120}{13}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{516}{143}\\y=-\dfrac{228}{143}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
c) \(\left\{{}\begin{matrix}x-y=2\\y-3z=2\\-3x-2y+z=-2\end{matrix}\right.\)
\(\Leftrightarrow\)\(\left\{{}\begin{matrix}x=y+2\\y=3z+2\\-3\left(y+2\right)-2\left(3z+2\right)+z=-2\end{matrix}\right.\)
\(\Leftrightarrow\)\(\left\{{}\begin{matrix}x=y+2\\y=3z+2\\-3y-6-6z-4+z=-2\end{matrix}\right.\)
\(\Leftrightarrow\)\(\left\{{}\begin{matrix}x=y+2\\y=3z+2\\-3y-5z=8\end{matrix}\right.\)\(\Leftrightarrow\)\(\left\{{}\begin{matrix}x=y+2\\y=3z+2\\-3\left(3z+2\right)-5z=8\end{matrix}\right.\)
\(\Leftrightarrow\)\(\left\{{}\begin{matrix}x=y+2\\y=3z+2\\-9z-6-5z=8\end{matrix}\right.\)\(\Leftrightarrow\)\(\left\{{}\begin{matrix}x=y+2\\y=3z+2\\-14z=14\end{matrix}\right.\)\(\Leftrightarrow\)\(\left\{{}\begin{matrix}x=\left(-1\right)+2=1\\y=3\left(-1\right)+2=-1\\z=-1\end{matrix}\right.\)
Vậy...
Đúng 0
Bình luận (0)
1.Giải hpt bằng pp đặt ẩn phụ ; 1\(\left\{{}\begin{matrix}x^2+y+x^3y+xy^2+xy=\dfrac{-5}{4}\\x^4+y^2+xy\left(1+2x\right)=\dfrac{-5}{4}\end{matrix}\right.\)
2.\(\left\{{}\begin{matrix}x^3+3x^2-13x-15=\dfrac{8}{y^3}-\dfrac{8}{y}\\y^2+4=5y^2\left(x^2+2x+2\right)\end{matrix}\right.\)
1.
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+y+x^3y+xy^2+xy=-\dfrac{5}{4}\\x^4+y^2+xy\left(1+2x\right)=-\dfrac{5}{4}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x^2+y\right)+xy+xy\left(x^2+y\right)=-\dfrac{5}{4}\\\left(x^2+y\right)^2+xy=-\dfrac{5}{4}\end{matrix}\right.\left(1\right)\)
Đặt \(\left\{{}\begin{matrix}x^2+y=a\\xy=b\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}a+b+ab=-\dfrac{5}{4}\\a^2+b=-\dfrac{5}{4}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-a^2-\dfrac{5}{4}-a\left(a^2+\dfrac{5}{4}\right)=-\dfrac{5}{4}\\b=-a^2-\dfrac{5}{4}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2-a^3-\dfrac{1}{4}a=0\\b=-a^2-\dfrac{5}{4}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-a\left(a^2-a+\dfrac{1}{4}\right)=0\\b=-a^2-\dfrac{5}{4}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a\left(a-\dfrac{1}{2}\right)^2=0\\b=-a^2-\dfrac{5}{4}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}a=0\\b=-\dfrac{5}{4}\end{matrix}\right.\\\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=-\dfrac{3}{2}\end{matrix}\right.\end{matrix}\right.\)
TH1: \(\left\{{}\begin{matrix}a=0\\b=-\dfrac{5}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2+y=0\\xy=-\dfrac{5}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{\sqrt[3]{10}}{2}\\y=-\dfrac{5}{2\sqrt[3]{10}}\end{matrix}\right.\)
TH2: \(\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=-\dfrac{3}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2+y=\dfrac{1}{2}\\xy=-\dfrac{3}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-\dfrac{3}{2}\end{matrix}\right.\)
Kết luận: Phương trình đã cho có nghiệm \(\left(x;y\right)\in\left\{\left(\dfrac{\sqrt[3]{10}}{2};-\dfrac{5}{2\sqrt[3]{10}}\right);\left(1;-\dfrac{3}{2}\right)\right\}\)
Đúng 1
Bình luận (0)
2.
\(\left\{{}\begin{matrix}\left(x+1\right)^3-16\left(x+1\right)=\left(\dfrac{2}{y}\right)^3-4\left(\dfrac{2}{y}\right)\\1+\left(\dfrac{2}{y}\right)^2=5\left(x+1\right)^2+5\end{matrix}\right.\)
Đặt \(\left\{{}\begin{matrix}x+1=u\\\dfrac{2}{y}=v\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u^3-16u=v^3-4v\\v^2=5u^2+4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u^3-v^3=16u-4v\\4=v^2-5u^2\end{matrix}\right.\)
\(\Rightarrow4\left(u^3-v^3\right)=\left(16u-4v\right)\left(v^2-5u^2\right)\)
\(\Leftrightarrow21u^3-5u^2v-4uv^2=0\)
\(\Leftrightarrow u\left(7u-4v\right)\left(3u+v\right)=0\Rightarrow\left[{}\begin{matrix}u=0\Rightarrow v^2=4\\u=\dfrac{4v}{7}\Rightarrow4=v^2-5\left(\dfrac{4v}{7}\right)^2\\v=-3u\Rightarrow4=\left(-3u\right)^2-5u^2\end{matrix}\right.\)
\(\Rightarrow...\)
Đúng 1
Bình luận (0)
\(\left(\dfrac{1}{5}x^3y\right).\left(-5xy^3\right)^0.\left(xy^3\right)^2=\)
lm hộ vs
\(=\dfrac{1}{5}x^3y\cdot x^2y^6=\dfrac{1}{5}x^5y^7\)
Đúng 5
Bình luận (1)
\(=\dfrac{1}{5}.\left(x^3x^2\right)\left(yy^{3.2}\right)=\dfrac{1}{5}x^5y^7\)
Đúng 4
Bình luận (1)
Xem thêm câu trả lời
Cho A = \(\dfrac{\left(x-y\right)^2+xy}{\left(x+y\right)^2-xy}.\left[1:\dfrac{x^5+y^5+x^3y^2+x^2y^3}{\left(x^3-y^3\right)\left(x^3+y^3+x^2y+xy^2\right)}\right]\)
B = x - y
Chứng minh đẳng thức A = B
Tính giá trị của A, B tại x = 0; y = 0 và giải thích vì sao A ≠ B
\(ĐK:x\ne y;x\ne-y;x^2+xy+y^2\ne0;x^2-xy+y^2\ne0\)
\(A=\dfrac{x^2-xy+y^2}{x^2+xy+y^2}\cdot\left[1:\dfrac{\left(x^3+y^3\right)\left(x^2+y^2\right)}{\left(x-y\right)\left(x^2+xy+y^2\right)\left(x+y\right)\left(x^2+y^2\right)}\right]\\ A=\dfrac{x^2-xy+y^2}{x^2+xy+y^2}\cdot\dfrac{\left(x-y\right)\left(x+y\right)\left(x^2+xy+y^2\right)\left(x^2+y^2\right)}{\left(x+y\right)\left(x^2-xy+y^2\right)\left(x^2+y^2\right)}\\ A=x-y=B\)
\(x=0;y=0\Leftrightarrow B=0\)
Giá trị của A không xác định vì \(x=y\) trái với ĐK:\(x\ne y\)
Vậy \(A\ne B\)
Đúng 1
Bình luận (0)