Nếu hai biến cố A và B xung khắc thì xác suất của biến cố P A ∪ B bằng
A. 1 - P A - P B
B. P A . P B - P A - P B
C. P A . P B
D. P A + P B
Nếu hai biến cố A và B xung khắc thì xác suất của biến cố P A ∪ B bằng
A. 1-P(A)-P(B)
B. P(A).P(B)
C. P(A).P(B)-P(A)-P(B)
D. P(A)+P(B)
Chứng minh các tính chất a), b) và c).
a) P ∅ = 0 , P Ω = 1 .
b) 0 ≤ P A ≤ 1 , với mọi biến cố A.
c) Nếu A và B xung khắc, thì
P A ∪ B = P A + P B (công thức cộng xác suất).
Theo định nghĩa xác suất của biến cố ta có:
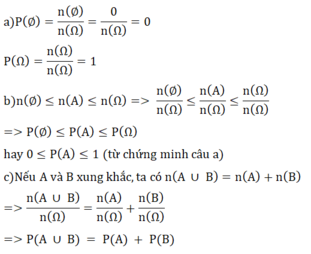
Cho hai biến cố A và B là hai biến cố xung khắc với P(A) > 0, P(B) > 0. Chứng tỏ rằng hai biến cố A và B không độc lập.
Hai biến cố A và B xung khắc khi và chỉ khi \(A \cap B = \emptyset \Rightarrow P\left( {AB} \right) = 0\)
Vì P(A) > 0, P(B) > 0 nên \(P\left( A \right).P\left( B \right) > 0\)
\( \Rightarrow P\left( {AB} \right) \ne P\left( A \right).P\left( B \right)\)
Vậy hai biến cố A và B không độc lập.
a) Hai biến cố đối nhau có xung khắc với nhau không?
b) Hai biến cố xung khắc có phải là hai biến cố đối nhau không?
a) Hai biến cố đối nhau không có xung khắc với nhau. Xung khắc xảy ra khi hai biến cố không thể xảy ra cùng một lúc.
b) Hai biến cố xung khắc không nhất thiết là hai biến cố đối nhau. Hai biến cố đối nhau xảy ra khi xảy ra một biến cố sẽ loại trừ hoàn toàn biến cố kia.
$HaNa$
Cho hai biến cố A và biến cố B. Biết xác suất để biến cố A xảy ra là 1/4, xác suất để biếncố B xảy ra là 1/3. Khẳng định nào sau đây đúng?
A. Biến cố A có khả năng xảy ra cao hơn biến cố B
B. Biến cố A và biến cố B đồng khả năng xảy ra
C. Biến cố A có khả năng xảy ra ít hơn biến cố B
D. Một kết quả khác
Cho hai biến cố xung khắc \(A\) và \(B\). Có 5 kết quả thuận lợi cho biến cố \(A\) và 12 kết quả thuận lợi cho biến cố \(B\). Hãy so sánh \(P\left( {A \cup B} \right)\) với \(P\left( A \right) + P\left( B \right)\).
Số kết quả thuận lợi cho biến cố \(A \cup B\) là \(5 + 12 = 17\).
\(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{5}{{n\left( \Omega \right)}};P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega\right)}} = \frac{{12}}{{n\left( \Omega\right)}};P\left( {A \cup B} \right) = \frac{{n\left( {A \cup B} \right)}}{{n\left( \Omega\right)}} = \frac{{17}}{{n\left( \Omega\right)}}\)
\( \Rightarrow P\left( A \right) + P\left( B \right) = P\left( {A \cup B} \right)\)
Cho các mệnh đề:
P
(
Ω
)
=
1
,
P
(
∅
)
=
0
;
0 < P ( A ) < 1 , ∀ A ≠ Ω ;
Với A, B là hai biến cố xung khắc thì P ( A ∪ B ) = P ( A ) + P ( B ) ;
Với A, B là hai biến cố bất kì thì P ( A B ) = P ( A ) . P ( B ) .
Tìm số mệnh đề đúng trong 4 mệnh đề trên.
A. 3
B. 4
C. 1
D. 2
An và Bình mỗi người gieo một con xúc xắc cân đối và đồng chất. Gọi \(A\) là biến cố “An gieo được mặt 6 chấm” và \(B\) là biến cố “Bình gieo được mặt 6 chấm”.
a) Tính xác suất của biến cố \(B\).
b) Tính xác suất của biến cố \(B\) trong hai trường hợp sau:
• Biến cố \(A\) xảy ra
• Biến có \(A\) không xảy ra.
a) Xác suất của biến cố B là \(\dfrac{1}{6}\), vì có 6 mặt trên xúc xắc và chỉ có duy nhất một mặt là mặt 6 chấm.
b)
+ Trong trường hợp biến cố A xảy ra, xác suất của biến cố B không thay đổi. Vì hai biến cố này là độc lập, kết quả của biến cố A không ảnh hưởng đến biến cố B.
+ Trong trường hợp biến cố A không xảy ra, tức là An không gieo được mặt 6 chấm, xác suất của biến cố B là \(\dfrac{1}{6}\)
$HaNa$
Tham khảo:
a) \(B=\dfrac{1}{6}\)
b) Biến cố A xảy ra: \(B=\dfrac{1}{6}\)
Biến cố A không xảy ra: \(B=\dfrac{1}{6}\)
Tại sao công thức cộng xác suất cho hai biến cố xung khắc là hệ quả của công thức cộng xác suất?
Vì hai biến cố A và B xung khắc khi và chỉ khi \(A \cap B = \emptyset \Rightarrow P\left( {AB} \right) = 0\)
Từ công thức cộng xác suất ta có \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\)
Vậy công thức cộng xác suất cho hai biến cố xung khắc là hệ quả của công thức cộng xác suất.