Hàm số y = tanx liên tục khoảng nào sau đây:

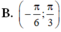
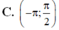
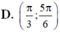
Hàm số y = tan x liên tục trên khoảng nào sau đây:
A. 5 π 4 ; 7 π 4
B. − π 6 ; π 3
C. − π ; π 2
D. π 3 ; 5 π 6
Hàm số nào sau đây liên tục trên toàn bộ tập số thực R
A/ f(X)=√x2+2x+1
B/ g(x)= 4x^2-5x^2+1
C/ h(x)= x-1/ x+1
D/ y= tanx
Nếu đề là \(f\left(x\right)=\sqrt{x^2+2x+1}\) và \(g\left(x\right)=4x^2-5x^2+1\left(???\right)\) thì cả \(f\left(x\right)\) và \(g\left(x\right)\) đều liên tục trên R
Cho hàm số y=f(x) có đạo hàm liên tục trên ~ , hàm số y=f’(x) có đồ thị hàm số như hình dưới đây
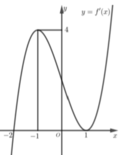
Hàm số y=f(x) đồng biến trên khoảng nào trong các khoảng sau:
A. (-∞;2); (1;+∞)
B. (-2;+∞)/{1}
C. (-2;+∞)
D. (-4;0)
Chọn C
Từ đồ thị hàm số y=f’(x) ta có bảng biến thiên cho hàm số y=f(x) như sau:
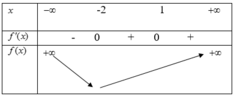
Nhìn vào bảng biến thiên ta thấy ngay trong khoảng (-2;+∞) thì hàm số y=f(x) đồng biến
Cho các hàm số y=sinx, y=cos x ( I ) và y= tanx(III). Hàm số nào liên tục trên R?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Chọn B
Ta có hàm số ![]() có tập xác định là
có tập xác định là ![]() nên liên tục trên
nên liên tục trên ![]() .
.
Hàm số ![]() có tập xác định là
có tập xác định là ![]() nên không liên tục trên
nên không liên tục trên ![]() .
.
Hàm số ![]() có tập xác định là
có tập xác định là ![]() nên không liên tục trên
nên không liên tục trên ![]() .
.
Cho hàm số y = f(x) có đạo hàm liên tục trên R. Đồ thị hàm số y = f ' x như hình bên dưới
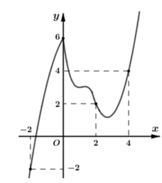
Hàm số g x = 2 f x − x 2 đồng biến trên khoảng nào trong các khoảng sau đây?
A. 2 ; + ∞ .
B. − ∞ ; − 2 .
C. (-2;2)
D. (2;4)
Cho hàm số f ( x ) = x 2 + 1 x 2 + 5 x + 6 Khi đó hàm số y = f(x) liên tục trên các khoảng nào sau đây?
A. (-3; 2).
B. (-2; +∞).
C. (-∞; 3).
D. (2; 3).
Chọn B.
Hàm số có nghĩa khi 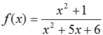 .
.
Vậy theo định lí ta có hàm số 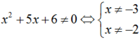 liên tục trên khoảng (-∞; -3); (-3; -2) và (-2; +∞).
liên tục trên khoảng (-∞; -3); (-3; -2) và (-2; +∞).
Cho hàm số y=f(x) liên tục và có bảng biến thiên như sau
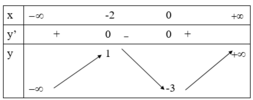
Hàm số y= f(x) nghịch biến trên khoảng nào dưới đây?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số y = f(x) liên tục và có bảng biến thiên như sau:
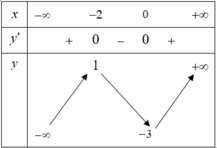
Hàm số y=f(x) nghịch biến trên khoảng nào dưới đây?
![]()
![]()
![]()
![]()
Cho hàm số y = f x liên tục trên ℝ . Biết rằng hàm số y = f ' x có đồ thị như hình bên. Hỏi hàm số y = f x 2 − 5 nghịch biến trên khoảng nào sau đây?

A. − 1 ; 0
B. 1 ; 2
C. − 1 ; 1
D. 0 ; 1
Đáp án D.
Dựa vào hình vẽ, ta thấy rằng
f ' x > 0 ⇔ x ∈ − 4 ; − 1 ∪ 2 ; + ∞ f ' x < 0 ⇔ x ∈ − ∞ ; − 4 ∪ − 1 ; 2
Ta có y = f x 2 − 5 ⇒ y ' = 2 x . f ' x 2 − 5 ; ∀ x ∈ ℝ
Lại có y ' < 0 ⇔ x . f ' x 2 − 5 < 0 ⇔ x > 0 f ' x 2 − 5 < 0 x < 0 f ' x 2 − 5 > 0 ⇔ x > 0 x 2 − 5 ∈ − ∞ ; − 4 ∪ − 1 ; 2 x < 0 x 2 − 5 ∈ − 4 ; − 1 ∪ 2 ; + ∞
(*)
Giải (*) suy ra hàm số y = f x 2 − 5 nghịch biến trên khoảng 0 ; 1 .