Cho hàm số![]() . Tìm m để đồ thị
. Tìm m để đồ thị ![]() có ba điểm cực trị tạo thành một tam giác có trọng tâm trùng với gốc tọa.
có ba điểm cực trị tạo thành một tam giác có trọng tâm trùng với gốc tọa.
A. ![]() .
.
B. ![]() .
.
C. ![]() hoặc
hoặc ![]() .
.
D.![]() .
.
Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số y = − x 4 + 2 m x 2 − 1 có 3 điểm cực trị tạo thành một tam giác có tâm đường tròn ngoại tiếp trùng với gốc tọa độ O.
A. m = 0 hoặc m = 1.
B. m = 1 hoặc m = − 1 + 5 2 .
C. m = 1 hoặc m = − 1 − 5 2 .
D. m = − 1 − 5 2 hoặc m = − 1 + 5 2 .
Đáp án B.
Có y ' = − 4 x 3 + 4 m x . y ' = 0 ⇔ x = 0 x = m c = − m (Có 3 cực trị nên m > 0 ).
3 điểm cực trị là A 0 ; − 1 ; B m ; m 2 − 1 ; C − m ; m 2 − 1 . O là tâm đường tròn ngoại tiếp
⇔ O A = O B = O C ⇔ 1 = m + m 2 − 1 2 ⇔ m 4 − 2 m 2 + m = 0 ⇔ m m − 1 m 2 + m − 1 = 0 ⇔ m = 1 m = − 1 + 5 2 (Ta chỉ lấy m > 0 .)
Cho hàm số y = x 4 - 2 m x 2 + 1 - m . Tìm tất cả các giá trị thực của m để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác nhận gốc tọa độ Olàm trực tâm
A. m=0
B. m=2
C. m=1
D. Không tồn tại m
Cho hàm số y = x 4 - 2 m x 2 + 1 - m . Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác nhận gốc tọa độ O làm trực tâm.
A. m = 1
B. m = 2
C. m = 0
D. m = -1
Cho hàm số y = x 4 - 2 m x 2 + 1 - m . Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác nhân gốc tọa độ O làm trực tâm.
A. m = -1
B. m = 0
C. m = 1
D. m = 2
Cho hàm số y = x 4 - 2 m x 2 + m - 1 . Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số có ba điểm cực trị tạo thành 1 tam giác nhận gốc tọa độ O làm trực tâm .
A. m = 4
B. m = 2
C. m = 3
D. m = 1
Chọn D
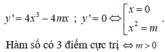
Khi đó đồ thị hàm số có 3 điểm cực trị là:
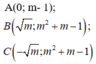
Vì B, C đối xứng với nhau qua trục tung nên B C ⊥ O A
Do đó O là trực tâm tam giác:
![]()
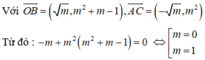
Kết hợp điều kiện, vậy m = 1 là giá trị cần tìm
Cho hàm số y = x 4 - 2 m x 2 + m - 1 . Tìm tất cả các giá trị của tham số thưc m để đồ thị hàm số có ba điểm cực trị tạo thành 1 tam giác nhận gốc tọa độ O làm trực tâm
A. m = 4.
B. m = 2.
C. m = 3.
D. m = 1.
Chọn D
y ' = 4 x 3 - 4 m x
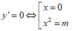
Hàm số có 3 điểm cực trị ⇔ m > 0
Khi đó đồ thị hàm số có 3 điểm cực trị là
A (0;m-1)
B ( m ; m 2 + m - 1 )
C ( - m ; m 2 + m - 1 )
Vì B,C đối xứng nhau qua trục tung nên B C ⊥ O A
Do đó O là trực tâm tam giác ABC
![]()
Với O B ⇀ = ( m , m 2 + m - 1 ) , A C ⇀ = ( - m , m 2 )
![]()
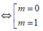
Vậy m = 1 là gtct
Cho hàm số y= x4-2mx2+ m-1. Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số có ba điểm cực trị tạo thành 1 tam giác nhận gốc tọa độ O làm trực tâm .
A. m=0
B. m=1
C. m= 1;2
D. m= 0;1
+ Đạo hàm y’ = 4x3- 4mx
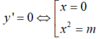
Hàm số có 3 điểm cực trị khi và chỉ khi m≠0.
+ Khi đó đồ thị hàm số có 3 điểm cực trị là:

+ Vì B,C đối xứng nhau qua trục tung nên BC và OA vuông góc với nhau.
Do đó O là trực tâm tam giác ABC khi và chỉ khi OB vuông góc AC hay ![]()
Với
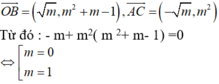
Kết hợp với điều kiện m ≠ 0 thì m = 1 là giá trị cần tìm.
Chọn B.
Cho hàm số \(y=x^4-2mx^2+m-1\left(1\right)\), với m là tham số thực.
Xác định m để hàm số (1) có 3 điểm cực trị, đồng thời các điểm cực trị của đồ thị tạo thành một tam giác biết :
a) Có bán kính đường tròn ngoại tiếp bằng 1
b) Có trực tâm là gốc tọa độ
c) Có trọng tâm là gốc tọa độ
Ta có \(y=4x^3-4mx=4x\left(x^2-m\right)=0\Leftrightarrow x=0\) hoặc \(x^2=m\)
Hàm số đã cho có 3 điểm cực trị \(\Leftrightarrow\) phương trình y' = 0 có 3 nghiệm phân biệt và y' đổi dấu khi x đi qua các nghiệm đó <=> m > 0. Khi đó 3 điểm cực trị của đồ thị hàm số là :
\(A\left(0;m-1\right);B\left(-\sqrt{m};m^2+m-1\right);C\left(\sqrt{m};-m^2+m-1\right)\)
a) Ta có \(S_{\Delta ABC}=\frac{1}{2}\left|y_B-y_A\right|.\left|y_C-y_B\right|=m^2\sqrt{m}\)
\(AB=AC=\sqrt{m^4+m};BC=2\sqrt{m}\)
\(R=\frac{AB.AC.BC}{4S_{\Delta ABC}}=1\Leftrightarrow\frac{\left(m^4+m\right)2\sqrt{m}}{4m^2\sqrt{m}}=1\)
\(\Leftrightarrow m^3-2m+1=0\Leftrightarrow m=1\) hoặc \(m=\frac{\sqrt{5}-1}{2}\)
Vậy \(m=1;m=\frac{\sqrt{5}-1}{2}\) là giá trị cần tìm
b) Vì B, C đối xứng nhau qua trục tung nên BC luôn vuông góc OA
Do đó O là trực tâm tam giác ABC khi và chỉ khi \(\overrightarrow{OB}.\overrightarrow{AC}=0\)
\(\overrightarrow{OB}\left(-\sqrt{m};-m^2+m-1\right);\overrightarrow{AC}\left(\sqrt{m};-m^2\right)\)
Suy ra \(-m-m^2\left(-m^2+m-1\right)=0\Leftrightarrow m\left(-m^3+m^2-m+1\right)=0\)
\(\Leftrightarrow m\left(m-1\right)\left(m^2+1\right)=0\Leftrightarrow m=0\) hoặc m = 1
Vậy m = 0 hoặc m = 1 là giá trị cần tìm
c) Rõ ràng tam giác ABC cân tại A và truyên tuyến kẻ từ A thuộc Oy. Do đó O là trọng tâm của tam giác ABC
<=> \(y_A+2y_B=0\)
\(\Leftrightarrow m-1+2\left(-m^2+m-1\right)=0\)
\(\Leftrightarrow2m^2-3m+3=0\) vô nghiệm
Vậy không tồn tai giá trị m thỏa mãn yêu cầu bài toán
Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = x 3 - 3 ( m + 1 ) x 2 + 12 m x - 3 m + 4 ( C ) có hai điểm cực trị là A và B sao cho hai điểm này cùng với điểm C - 1 ; - 9 2 lập thành tam giác nhận gốc tọa độ O làm trọng tâm
A. m = 1 2
B. m = - 2
C. m = 2
D. m = - 1 2
Chọn D
T a c ó y ' = 3 x 2 - 6 ( m + 1 ) x + 12 m
Hàm số có hai cực trị ⇔ y ' = 0 có hai nghiệm phân biệt
![]()
A ( 2 ; 9 m ) , B ( 2 m - 4 m 3 + 12 m 2 - 3 m + 4 )
ABC nhận O làm trọng tâm
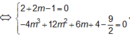
![]()