Bài 10: Cho hình bình hành ABCD. Biết  = 1240.
a) Tính các góc của hình bình hành;
b) Gọi E, F lần lượt là trung điểm của AB và CD. Chứng minh: AF // CE;
c) Gọi O là trung điểm của AC. Chứng minh: E và F đối xứng nhau qua O.

Những câu hỏi liên quan
tính số đo các góc của hình bình hành ABCD biết Â+góc B+ góc C=230 độ
Xét h.b.h ABCD
có: ^A + ^B + ^C + ^D = 360 độ
=> ^D = 130
mà ^A + ^D = 180 độ ( trong cùng phía)
=> ^A = 50 độ
mà ^A = ^C = 50 độ ( ABCD là h.b.h; ^A và ^C là 2 góc đối)
=> ^C = 50 độ
^D = ^B = 130 độ ( 2 góc đối)
=> ^B = 130 độ
Đúng 0
Bình luận (0)
xét hình bình hành ABCD,ta có:
góc A+ góc B +góc C +góc D=360o
mà góc A+ góc B +góc C=230o
=>góc D=360-230=130o
mà góc A+góc D=180o
=>góc A=180-130=50o
do góc A và góc C là hai góc đối =>góc A+góc C=180o=>góc C=180o-50o=130o
do góc B và góc D là hai góc đối =>góc B+góc D=180o=>góc B=180o-130o=50o
vậy góc A=50o
góc B=50o
góc C=150o
góc D=150o
Đúng 0
Bình luận (0)
câu 10 cho hình bình hành ABCD (AB//GÓC D=130\(^0\)
CD và góc B - góc C =50\(^0\)hãy tính các góc còn lại của hình thang
câu 11 cho hình bình hành ABCD có góc A =3 lần góc B.Hãy tính số đo góc của hình bình hành
Câu 10:
góc A=180-130=50 độ
góc B=(180+50)/2=230/2=115 độ
góc C=180-115=65 độ
Đúng 1
Bình luận (0)
Bài 1Cho hình bình hành ABCD gọi E là trung điểm của AD, F là trung điểm của ACa) chứng minh DE DF b) Chứng minh EBFC là hình bình hành c) Chứng minh EF, BD, AC đồng quyBài 2Cho hình bình hành ABCD kẻ AH , CK vuống góc với đường chéo BDCH , K thuộc BDa) Chứng minh AH CKB) Chứng minh AHCK là hình bình hànhBài 3 Tính các góc của hình bình hành ABCD biết góc A - góc B 10 độBài 4 Tứ giác ABCD gọi E, F, G, H là trung điểm của BD, AB, AC, CDa) chứng minh EF, GH là hình bình hànhb) tính chu vi của h...
Đọc tiếp
Bài 1
Cho hình bình hành ABCD gọi E là trung điểm của AD, F là trung điểm của AC
a) chứng minh DE = DF
b) Chứng minh EBFC là hình bình hành
c) Chứng minh EF, BD, AC đồng quy
Bài 2
Cho hình bình hành ABCD kẻ AH , CK vuống góc với đường chéo BDCH , K thuộc BD
a) Chứng minh AH =CK
B) Chứng minh AHCK là hình bình hành
Bài 3
Tính các góc của hình bình hành ABCD biết góc A - góc B = 10 độ
Bài 4
Tứ giác ABCD gọi E, F, G, H là trung điểm của BD, AB, AC, CD
a) chứng minh EF, GH là hình bình hành
b) tính chu vi của hình bình hành EFGH biết AD = 12, BC =16
Mk đag cần gấp mn giúp mk vs
Cho hình bình hành ABCD có góc a = 3 góc B . Tính số đo các góc của hình bình hành
\(\widehat{A}=\widehat{C}=135^0\)
\(\widehat{B}=\widehat{D}=45^0\)
Đúng 0
Bình luận (0)
Bài 5. Cho hình bình hành ABCD ( Â > 900). Vẽ ra ngoài hình bình hành các tam giác đều ADE và ABF. Chứng minh : rCEF là tam giác đều.
Tính diện tích hình bình hành ABCD biết góc Â= 135o ,AD= √2 dm, CD= 3 dm
Theo tính chất hình bình hành, \(\widehat{A}+\widehat{D}=180^0\Rightarrow\widehat{D}=45^0\)
Từ A kẻ AH vuông góc CD
Trong tam giác vuông ADH: \(\widehat{D}+\widehat{DAH}=90^0\Rightarrow\widehat{DAH}=45^0\)
\(\Rightarrow\widehat{DAH}=\widehat{D}\Rightarrow\Delta DAH\) vuông cân tại H \(\Rightarrow AH=DH\)
Áp dụng Pitago:
\(AH^2+DH^2=AD^2\Rightarrow2AH^2=2\)
\(\Rightarrow AH=1\)
\(\Rightarrow S_{ABCD}=AH.CD=1.3=3\left(dm^2\right)\)
Đúng 1
Bình luận (0)
Tính diện tích hình bình hành ABCD biết góc Â= 135o ,AD= √2 dm, CD= 3 dm
Cho hình bình hành ABCD, AB= 10cm, AD= 6cm, góc A > góc B. Tính số đo các góc của hình bình hành ABCD.
mình dốt hình lắm chỉ biết số học thôi
CHÚC BẠN HỌC GIỎI
TK MÌNH NHÉ
Đúng 0
Bình luận (0)
Tính các góc của hình bình hành biết: Â= 100°, Góc A - góc B= 30°. Các bn nào giỏi giải giúp mình đi ạ, mình cảm ơn
a: \(\widehat{B}=\widehat{D}=80^0\)
\(\widehat{C}=100^0\)
b: \(\widehat{A}=\widehat{C}=105^0\)
\(\widehat{B}=\widehat{D}=75^0\)
Đúng 0
Bình luận (1)
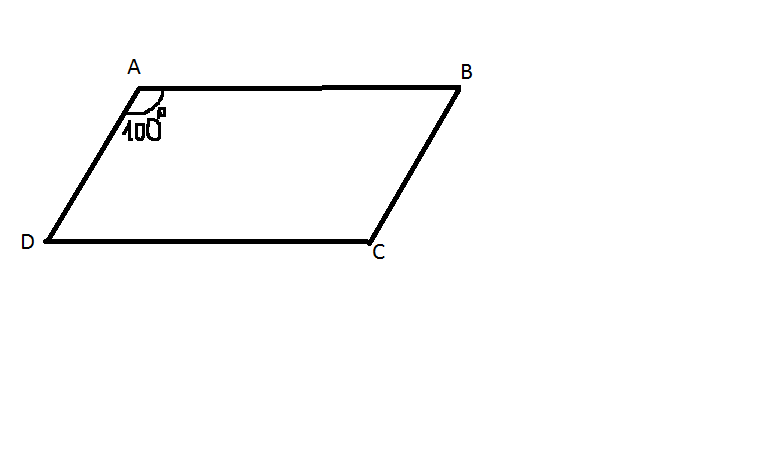
\(\widehat{A}=\widehat{C}=100^o\)(hai cặp góc đối trong hình bình hành thì bằng nhau)
Do\(AB//DC\) \(\Rightarrow\widehat{A}+\widehat{D}=180^o\) (hai góc bù nhau)\(\Rightarrow\widehat{D}=180^o-100^o=80^o\)
\(\widehat{B}=\widehat{D}=80^o\)(hai cặp góc đối trong hình bình hành thì bằng nhau)
Đúng 1
Bình luận (0)





















