Tổng số đo các góc ngoài của một tam giác bằng
(mỗi đỉnh tính 1 góc ngoài)

Những câu hỏi liên quan
Cho tam giác ABC có A = 90 độ và B-C=20 độ
a. Tính số đo các góc và .
b. Chứng tỏ tổng số đo các góc ngoài ở ba đỉnh của một tam giác bằng 1800.
a. B = 55 độ
C = 35
b. lỗi. phải là 360 độ
ông họ ngô
tôi họ đinh
Đúng 4
Bình luận (0)
Chứng tỏ tổng số đo các góc ngoài ở ba đỉnh của một tam giác bằng 3600.
Lời giải:
Gọi $\widehat{A}, \widehat{B}, \widehat{C}$ là 3 góc trong tam giác $ABC$ và $\widehat{A_1}, \widehat{B_1}, \widehat{C_1}$ tương ứng là 3 góc ngoài 3 đỉnh.
Ta có:
$\widehat{A_1}+\widehat{B_1}+\widehat{C_1}=(180^0-\widehat{A})+(180^0-\widehat{B})+(180^0-\widehat{C})$
$=540^0-(\widehat{A}+\widehat{B}+\widehat{C})$
$=540^0-180^0=360^0$
Đúng 2
Bình luận (0)
a) Góc ngoài của một tam giác cân có số đo bằng 1300 . Tính số đo các góc tam giác đó. b) Góc ngoài của một tam giác cân có số đo bằng 800 . Tính số đo các góc tam giác đó.
cho tam giác ABC tại mỗi đingr vẻ một góc ngoài của tam giác tính tổng số đo 3 góc ngoài
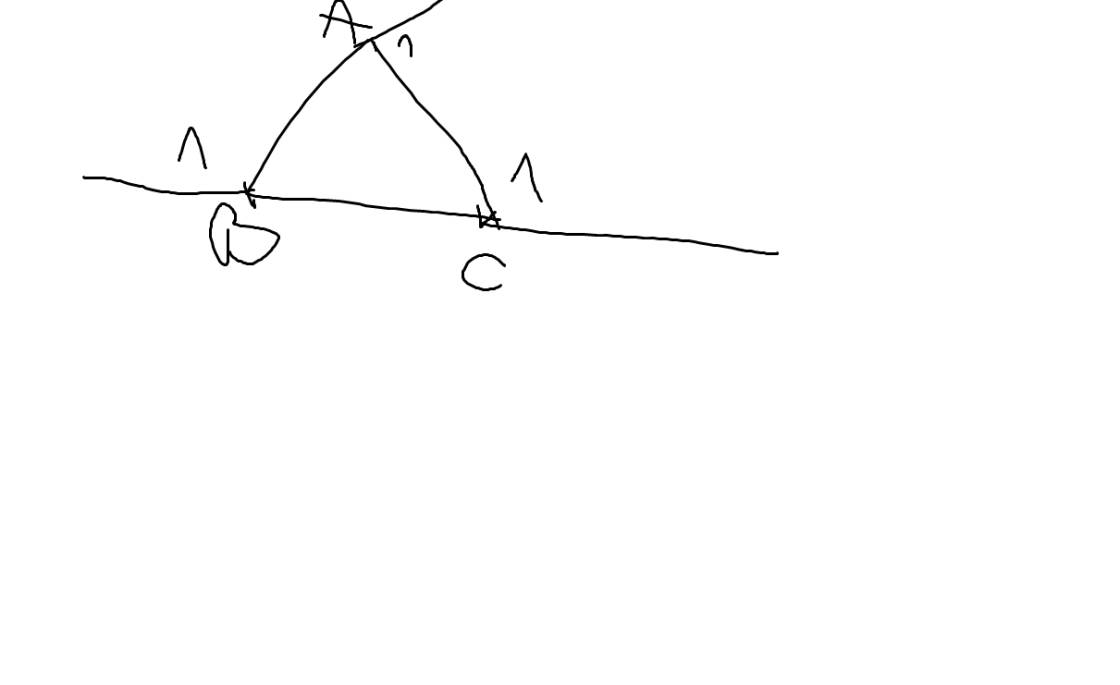
Gọi \(\widehat{A_1};\widehat{B_1};\widehat{C_1}\) lần lượt là các góc ngoài tại các đỉnh A,B,C của ΔABC
Xét ΔABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)
\(\widehat{B_1}+\widehat{ABC}=180^0\)(hai góc kề bù)
=>\(\widehat{B_1}=180^0-\widehat{ABC}\)
\(\widehat{C_1}+\widehat{ACB}=180^0\)(hai góc kề bù)
=>\(\widehat{C_1}=180^0-\widehat{ACB}\)
\(\widehat{A_1}+\widehat{BAC}=180^0\)(hai góc kề bù)
=>\(\widehat{A_1}=180^0-\widehat{BAC}\)
\(\widehat{A_1}+\widehat{B_1}+\widehat{C_1}\)
\(=180^0-\widehat{BAC}+180^0-\widehat{ABC}+180^0-\widehat{ACB}\)
\(=540^0-180^0=360^0\)
Đúng 1
Bình luận (0)
Một đa giác đều có tổng số đo tất cả các góc ngoài (tại mỗi đỉnh của đa giác lấy một góc ngoài) và một góc trong của đa giác bằng 468 O.
Vậy đa giác đó tất cả có bao nhiêu cạnh?
Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác. a) Tính các góc ngoài của tứ giác ở hình 7a. b) Tính tổng các góc ngoài của tứ giác ở hình 7b (tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài): c) Có nhận xét gì về tổng các góc ngoài của tứ giác?
Đọc tiếp
Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác.
a) Tính các góc ngoài của tứ giác ở hình 7a.
b) Tính tổng các góc ngoài của tứ giác ở hình 7b (tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài):
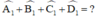
c) Có nhận xét gì về tổng các góc ngoài của tứ giác?
a) + Góc ngoài tại A là góc A1:
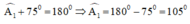
+ Góc ngoài tại B là góc B1:
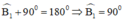
+ Góc ngoài tại C là góc C1:

+ Góc ngoài tại D là góc D1:
Theo định lý tổng các góc trong một tứ giác bằng 360º ta có:
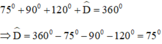
Lại có:
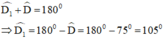
Vậy góc ngoài tại D bằng 105º.
b) Hình 7b:
Ta có:
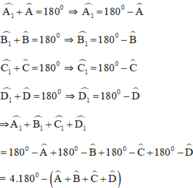
Mà theo định lý tổng bốn góc trong một tứ giác bằng 360º ta có:
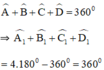
c) Nhận xét: Tổng các góc ngoài của tứ giác cũng bằng 360º.
Đúng 1
Bình luận (0)
Tính tổng các góc ngoài của tứ giác (tai mỗi đỉnh của tứ giác chỉ chọn một góc ngoài).
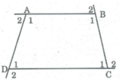
Ta có: ∠ A 1 + ∠ B 1 + ∠ C 1 + ∠ D 1 = 360 o (tổng các góc của tứ giác)
+) Lại có: ∠ A 1 + ∠ A 2 = 180 o ( hai góc kề bù).
∠ B 1 + ∠ B 2 = 180 o (hai góc kề bù)
∠ C 1 + ∠ C 2 = 180 o (hai góc kề bù)
∠ D 1 + ∠ D 2 = 180 o (hai góc kề bù)
Suy ra: ∠ A 1 + ∠ A 2 + ∠ B 1 + ∠ B 2 + ∠ C 1 + ∠ C 2 + ∠ D 1 + ∠ D 2 = 180 0 . 4 = 720 0
⇒ ∠ A 2 + ∠ B 2 + ∠ C 2 + ∠ D 2 = 720 0 - ∠ A 1 + ∠ B 1 + ∠ C 1 + ∠ D 1
= 720 0 - 360 0 = 360 0
Đúng 0
Bình luận (0)
1. Cho tam giác ABC có góc A bằng 74 độ góc B bằng 47 độ. Tính số đo góc ngoài tại đỉnh C?
2. Cho tam giác DEF có góc F bằng 40 độ, D - E bằng 52 độ. Tính số đo góc D, góc E?
3. Cho tam giác ABC có góc A bằng x, số đo góc B bằng 2x, số đo góc C bằng 3x. Tính số đo các góc của tam giác ABC
Bài 1:
Số đo góc ngoài tại đỉnh C là \(74^0+47^0=121^0\)
Câu 2:
Đặt \(\widehat{D}=a;\widehat{E}=b\)
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}a-b=52\\a+b=140\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=96\\b=44\end{matrix}\right.\)
Bài 3:
Theo đề, ta có: x+2x+3x=180
=>6x=180
=>x=30
=>\(\widehat{A}=30^0;\widehat{B}=60^0;\widehat{C}=90^0\)
Đúng 0
Bình luận (0)
Tính tổng các góc ngoài của tứ giác ( tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài).
4 góc tứ giác là a,b,c,d
=.4 góc ngoài =180-a,180-b,180-c,180-d
=>tổng chúng =720độ - 360 độ=360 độ
Đúng 0
Bình luận (0)
Gọi 4 góc của tứ giác là : a , b , c , d
Thì 4 góc ngoài của tứ giác lần lượt là : 180 - a ; 180 - b ; 180 - c ; 180 - d
Vậy 4 góc ngoài của tứ giác là : 180 - a + 180 - b + 180 - c + 180 - d
= ( 180 + 180 + 180 + 180 ) - ( a + b + c + d )
= 720o - 360o ( tổng 4 góc của tứ giác )
= 360o
Vậy tổng 4 góc ngoài của tứ giác là 360o
Đúng 0
Bình luận (0)
Xem thêm câu trả lời


















