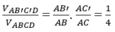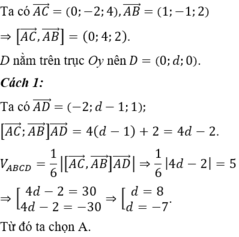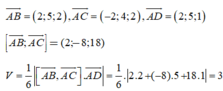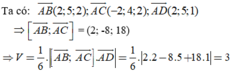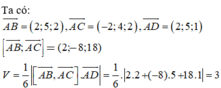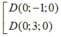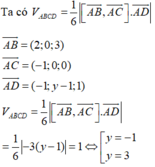Cho tứ diện ABCD có thể tích V. Gọi A 1 B 1 C 1 D 1 là tứ diện với các đỉnh lần lượt là trọng tâm tam giác BCD, CDA, DAB, ABC và có thể tích V 1 . Gọi A 2 B 2 C 2 D 2 là tứ diện với các đỉnh lần lượt là trọng tâm tam giác B 1 C 1 D 1 , C 1 D 1 A 1 , D 1 A 1 B 1 , A 1 B 1 C 1 và có thể tích V 2 … cứ như vậy cho tứ diện A n B n C n D n có thể tích V n với n là số tự nhiên lớn hơn 1. Tính giá trị của biểu thức P = lim n → + ∞ V + V 1 + ... + V n .
A. 27 26 V
B. 1 27 V
C. 9 8 V
D. 82 81 V