Cho hình chóp S.ABCD có SA vuông góc với đáy và đáy ABCD là hình chữ nhật. Biết
A B = 4 a , A D = 3 a , S B = 5 a . Tính khoảng cách từ điểm C đến mp (SBD)
A. 12 41 41
B. 41 a 12
C. 12 61 a 61
D. 61 a 12
Cho hình chóp S.ABCD có SA vuông góc với đáy và đáy ABCD là hình chữ nhật. Biết AB =4a,AD=3a,B=5a. Tính khoảng cách từ điểm C đến mp (SBD)
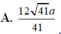
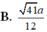
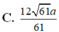
Chọn A
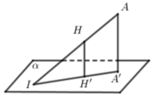
Phương pháp:
Sử dụng lý thuyết:
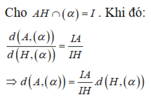
Cách giải:
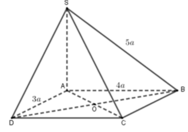
cho hình chóp s abcd có đáy abcd là hình chữ nhật AB=3a bc=4a sa=5a và SA vuông góc với mặt phẳng ABCD. Tính theo a khoảng cách từ điểm C đến mặt phẳng SBD
Cho hình chóp S.ABCD có đáy là hình chữ nhật. AD = 2a. AB = 4a. SD = 5a. SA vuông góc với mặt phẳng đáy. Gọi M là trung điểm của BC, N thuộc SB sao cho SN= 1/3 SB. Tính khoảng cách từ N đến mp (SMD)
Nối DM và AB kéo dài cắt nhau tại E
Do BM song song và bằng 1 nửa AD \(\Rightarrow BM\) là đường trung bình tam giác ADE
\(\Rightarrow AE=2BE\Rightarrow d\left(B;\left(SMD\right)\right)=\dfrac{1}{2}d\left(A;\left(SMD\right)\right)\)
Lại có: \(\left\{{}\begin{matrix}BN\cap\left(SMD\right)=S\\NS=\dfrac{1}{3}BS\end{matrix}\right.\) \(\Rightarrow d\left(N;\left(SMD\right)\right)=\dfrac{1}{3}d\left(B;\left(SMD\right)\right)=\dfrac{1}{6}d\left(A;\left(SMD\right)\right)\)
Từ A kẻ AF vuông góc MD (F thuộc MD), từ A kẻ AH vuông góc SF (H thuộc SF)
\(\Rightarrow AH\perp\left(SMD\right)\Rightarrow AH=d\left(A:\left(SMD\right)\right)\)
Hệ thức lượng trong tam giác vuông ADE:
\(\Rightarrow AF=\dfrac{AD.AE}{DE}=\dfrac{AD.2AB}{\sqrt{AD^2+\left(2AB\right)^2}}=\dfrac{8a\sqrt{17}}{17}\)
\(SA=\sqrt{SD^2-AD^2}=a\sqrt{21}\)
Hệ thức lượng: \(AH=\dfrac{SA.AF}{\sqrt{SA^2+AF^2}}=...\)
\(\Rightarrow d\left(N;\left(SMD\right)\right)=\dfrac{1}{6}AF=...\)
Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật. Cạnh SA vuông góc với mặt phẳng A B C D . Biết A B = a , A D = 2 a , góc giữa cạnh bên SD và mp A B C D bằng 60 ° . Tính khoảng cách từ A đến mp S B D .
A. a 3 3
B. 2 a 6
C. a 2 3
D. a 3 2
Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật. Cạnh SA vuông góc với mặt phẳng (ABCD). Biết AB = a, AD = 2a, góc giữa cạnh bên SD và mp (ABCD) bằng 60 ° . Tính khoảng cách từ A đến mp (SBD).
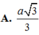
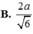
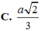
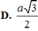
Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật. Cạnh SA vuông góc với mặt phẳng (ABCD). Biết AB = a , AD = 2 a , góc giữa cạnh bên SD và mp(ABCD) bằng 60 0 . Tính khoảng cách từ A đến mp(SBD).
A. a 2 3
B. a 3 3
C. a 3 2
D. 2 a 6
\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SBA}\) là góc giữa SB và (ABCD)
\(\Rightarrow\widehat{SBA}=45^0\Rightarrow SA=AB.tan45^0=a\)
Gọi O là tâm đáy \(\Rightarrow AO=CO\Rightarrow d\left(C;\left(SBD\right)\right)=d\left(A;\left(SBD\right)\right)\)
Kẻ AH vuông góc BD, kẻ AK vuông góc SH
\(\Rightarrow AK\perp\left(SBD\right)\Rightarrow AK=d\left(A;\left(SBD\right)\right)\)
\(\dfrac{1}{AH^2}=\dfrac{1}{AD^2}+\dfrac{1}{AB^2}=\dfrac{1}{a^2}+\dfrac{1}{4a^2}=\dfrac{5}{4a^2}\)
\(\dfrac{1}{AK^2}=\dfrac{1}{SA^2}+\dfrac{1}{AK^2}=\dfrac{1}{a^2}+\dfrac{5}{4a^2}=\dfrac{9}{4a^2}\)
\(\Rightarrow AK=\dfrac{2a}{3}\Rightarrow d\left(C;\left(SBD\right)\right)=\dfrac{2a}{3}\)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AC=a căn 3, BC = 2a, SA vuông góc (ABCD), SA=3a. Gọi O là giao điểm của AC và BD. a) Tính góc giữa mp ( SAB) và mp (SBC). b) Tính khoảng cách từ A đến mp ( SBD)
Tuy nhiên đề cho giá trị cạnh AC với BC bị sai. Cạnh huyền AC (\(a\sqrt{3}\)) sao lại có giá trị nhỏ hơn cạnh góc vuông BC (2a) nhỉ?
