Chọn A
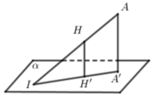
Phương pháp:
Sử dụng lý thuyết:
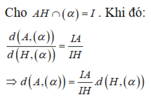
Cách giải:

Chọn A

Phương pháp:
Sử dụng lý thuyết:
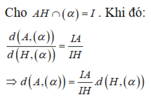
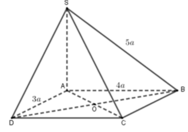
Cách giải:


cho hình chóp s abcd có đáy abcd là hình chữ nhật AB=3a bc=4a sa=5a và SA vuông góc với mặt phẳng ABCD. Tính theo a khoảng cách từ điểm C đến mặt phẳng SBD
Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật. Cạnh SA vuông góc với mặt phẳng (ABCD). Biết AB = a, AD = 2a, góc giữa cạnh bên SD và mp (ABCD) bằng 60 ° . Tính khoảng cách từ A đến mp (SBD).
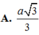
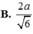
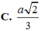
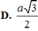
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với đáy. Biết khoảng cách từ A đến mặt phẳng (SBD) bằng a 3 Tính khoảng cách từ C đến mặt phẳng (SBD).
![]()
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Biết SA vuông góc với đáy và SA=a. Tính khoảng cách từ điểm A đến mp(SBD).
A. 2 a 3
B. a 3
C. a 2 3
D. a 2 6
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB 2a; BC = \(\dfrac{3a}{2}\); AD = 3a. Hình chiếu vuông góc của S lên (ABCD) l;à trung điểm H của BD. Biết góc giữa (SCD) và (ABCD) bằng 60 độ. Tình khoảng cách từ C đến (SBD)?
Cho hình chóp S. ABCD có đáy là hình vuông cạnh a. Biết SA vuông góc với đáy và SA =a.Tính khoảng cách từ điểm A đến mp (SBD)
A. 2 a 3
B. a 3
C. a 2 3
D. a 2 6
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, cạnh bên SA vuông góc với đáy. Biết khoảng cách từA đến mặt phẳng (SBD) bằng 6 a 7 . Khoảng cách từ điểm C đến mặt phẳng (SBD) bằng
A. 3 a 7
B. 4 a 7
C. 6 a 7
D. 12 a 7
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a. Biết SA vuông góc với mặt phẳng đáy và SA = 3a. Thể tích hình chóp S.ABCD là:
A. 6 a 3
B. 12 a 3
C. 2 a 3
D. 1 3 a 3
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, AD = a, AB = 2a, BC = 3a, SA = 2a. H là trung điểm cạnh AB, SH là đường cao của hình chóp S.ABCD, Tính khoảng cách từ điểm A đến mp (SCD)
A . a 30 7
B . a 30 10
C . a 13 10
D . a 13 7