Tất cả các nghiệm của phương trình tan x + 3 cot x − 3 − 1 = 0 là
A. x = π 4 + k π x = π 3 + k π k ∈ ℤ
B. x = − π 4 + k π x = π 6 + k π k ∈ ℤ
C. x = π 4 + k 2 π x = π 6 + k 2 π k ∈ ℤ
D. x = π 4 + k π x = π 6 + k π k ∈ ℤ
Những câu hỏi liên quan
Tất cả các nghiệm của phương trình
tan
x
+
3
.
c
o
t
x
-
3
-
1
0
là
Đọc tiếp
Tất cả các nghiệm của phương trình tan x + 3 . c o t x - 3 - 1 = 0 là
Tất cả các nghiệm của phương trình
tan
x
c
o
t
x
là A.
x
π
4
+
k
π
4
,
k
∈
ℤ
B.
x
π
4
+
k
2
π
,...
Đọc tiếp
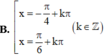
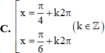
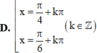
Tất cả các nghiệm của phương trình tan x = c o t x là
A. x = π 4 + k π 4 , k ∈ ℤ
B. x = π 4 + k 2 π , k ∈ ℤ
C. x = π 4 + k π , k ∈ ℤ
D. x = π 4 + k π 2 , k ∈ ℤ
Phương trình tan x cot x có tất cả các nghiệm là:
Đọc tiếp
Phương trình tan x = cot x có tất cả các nghiệm là:
Tổng tất cả các nghiệm của phương trình
3
cos
x
-
1
0
trên đoạn
0
;
4
π
là : A.
15
π
2
B.
6
π
C.
17...
Đọc tiếp
Tổng tất cả các nghiệm của phương trình 3 cos x - 1 = 0 trên đoạn 0 ; 4 π là :
A. 15 π 2
B. 6 π
C. 17 π 2
D. 8 π
Câu 1 : Giá trị lớn nhất của biểu thức P= 3 sin x +4 cosx là
Câu 2: Tính giá trị của biểu thức P=(sin²x-1)tan²x+ (cos²x-1)cot²x
Câu 3: Tìm các giá trị của tham số m để phương trình (x-2)(x-2mx+1)=0 có 2 nghiệm phân biệt
Xem chi tiết
1) nghiệm dương nhỏ nhất của phương trình \(cot\left(x-\dfrac{\pi}{6}\right)=\sqrt{3}\) là
2) phương trình \(sin\left(\dfrac{2x}{3}+\dfrac{\pi}{3}\right)=0\) có nghiệm là
3) họ nghiệm của phương trình \(cot\)(2x - 30 độ) = \(\sqrt{3}\) là
Cho phương trình: x^3 - x^2 - 9x - 9m= 0 , trong đó m là một số cho trước. Biết x = 3 là một nghiệm của phương trình. Tìm tất cả các nghiệm của phương trình.
x = 3 là nghiệm của phương trình, ta có:
3^3 - 3^2 - 9.3 - 9m = 0
<=> 27 - 9 - 27 - 9m = 0
<=> -9 - 9m = 0
<=> -9m = 0 + 9
<=> -9m = 9
<=> m = -1
phương trình tan^x+cot^x-3(tanx+cotx)-2=0 có bao nhiêu nghiệm thuộc(0,pi)
Gọi S là tập hợp tất cả các nghiệm của phương trình
3
tan
π
6
-
x
+
tan
x
.
tan
π
6
-
x
+
3
.
tan
x
tan
2
x
trên đoạn...
Đọc tiếp
Gọi S là tập hợp tất cả các nghiệm của phương trình 3 tan π 6 - x + tan x . tan π 6 - x + 3 . tan x = tan 2 x trên đoạn 0 ; 10 π . Số phần tử của S là.
A. 19
B. 20
C. 21
D. 22
Chọn B.
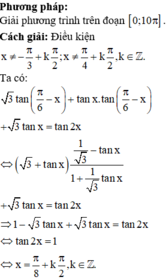
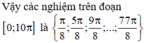
Vậy có 20 nghiệm thỏa mãn yêu cầu bài toán.
Đúng 0
Bình luận (0)
Gọi S là tập hợp tất cả các nghiệm của phương trình
3
tan(
π
6
-
x) + tanx.tan(
π
6
-
x) +
3
tanx tan2x trên đoạn [0;10π]. Số phần tử của S là: A. 19 B. 20 C. 21 D. 22
Đọc tiếp
Gọi S là tập hợp tất cả các nghiệm của phương trình 3 tan( π 6 - x) + tanx.tan( π 6 - x) + 3 tanx = tan2x trên đoạn [0;10π]. Số phần tử của S là:
A. 19
B. 20
C. 21
D. 22
Đáp án B
Phương pháp: Sử dụng công thức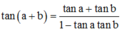 
Cách giải:
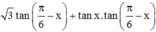
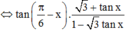
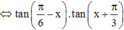
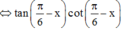
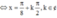
Ứng với mỗi giá trị của k ta có 1 nghiệm x.
Vậy số phần tử của S là 20.
Đúng 0
Bình luận (0)