Cho a,b là các số thực dương thỏa mãn a 2 b = 5 tính K = 2 a 6 b − 4
A. K=226
B. K=246
C. K=242
D. K=202
Cho a,b,c là các số dương thỏa mãn a^2+b^2+c^2 +6=2(a+2b+c).Tính K=√2a+3b+c
A,K=6
B,K=2
C,K=3
D,K=8
Lời giải:
$a^2+b^2+c^2+6=2(a+2b+c)$
$\Leftrightarrow (a^2-2a+1)+(b^2-4b+4)+(c^2-2c+1)=0$
$\Leftrightarrow (a-1)^2+(b-2)^2+(c-1)^2=0$
Vì $(a-1)^2\geq 0; (b-2)^2\geq 0; (c-1)^2\geq 0$ với mọi $a,b,c\in\mathbb{R}$ nên để tổng của chúng bằng $0$ thì:
$(a-1)^2=(b-2)^2=(c-1)^2=0$
$\Rightarrow a=c=1; b=2$
$\Rightarrow K=3$
Đáp án C.
Cho a, b là các số thực dương thỏa mãn a ≠ 1 , a ≠ b và log a b = 2 . Tính P = log b a a b .
A. P = 1 - 2 2 2 - 1
B. P = 1 + 2 2 2 + 1
C. P = 1 - 2 2 2 + 1
D. P = 1 + 2 2 2 - 1
Đáp án A
Ta có P = 1 2 . 1 - log a b log a b - 1 2 = 1 - 2 2 2 - 1 .
Cho a, b là các số thực dương thỏa mãn a ≠ 1 , a ≠ b và log a b = 2 . Tính P = log b a a b
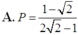
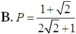
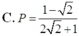
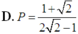
Các Ctv hoặc các giáo viên helpp ạ
Cho a,b,c là số thực dương không âm thỏa mãn
Cho a,b,c là số thực dương không âm thỏa mãn \(a+b+c=1\) . Chứng minh rằng :
\(\dfrac{1}{a^2+b^2}+\dfrac{1}{b^2+c^2}+\dfrac{1}{c^2+a^2}>10\)
Cho a, b là các số thực dương thỏa mãn a ≠ 1 , a ≠ 1 b và log a b = 5 . Tính P = log a b b a .
A. P = 11 − 3 5 4
B. P = 11 + 3 5 4
C. P = 11 − 2 5 4
D. P = 11 + 3 5 2
Đáp án A
Ta có: P = log a b b a = 2 log a b b a
= 2 log a b b − log a b a = 2 1 log b a b − 1 2 log a b a
= 2 1 1 + log b a − 1 2 . 1 log a a b = 2 1 1 + 1 log a b − 1 2 . 1 1 + log a b = 2 1 1 + 1 5 − 1 2 . 1 1 + 5 = 11 − 3 5 4
Cho a, b là các số thực dương thỏa mãn a ≠ 1 , a ≠ 1 b và log a b = 5 . Tính P = log a b b a .
A. P = 11 − 3 5 4
B. P = 11 + 3 5 4
C. P = 11 − 2 5 4
D. P = 11 + 3 5 2
Đáp án A
Ta có
P = log a b b a = 2. log a b b a = 2 log a b b − log a b a = 2 1 log b a b − 1 2 log a b a
= 2 1 1 + log b a − 1 2 . 1 log a a b = 2 1 1 + 1 log a b − 1 2 . 1 1 + log a b = 2 1 1 + 1 5 − 1 2 . 1 1 + 5 = 11 − 3 5 4 .
Cho a, b là các số thực dương thỏa mãn a ≠ 1 , a ≠ 1 b và log a b = 5 . Tính P = log a b b a .
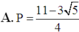
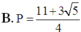
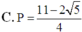
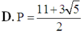
1. Cho \(x,y,z>1\) và \(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=2\) . Cmr \(\sqrt{x+y+z}\ge\sqrt{x-1}+\sqrt{y-1}+\sqrt{z-1}\)
2. Cho a,b,c là các số thực dương thỏa mãn \(a+b+c=6\) . Tính Min của \(A=\dfrac{a^2}{b+c}+\dfrac{b^2}{a+c}+\dfrac{c^2}{a+b}\)
3. Cho a,b,c là các số thực dương thỏa mãn \(a^2+b^2+c^2=1\) . Tính min của \(B=a+b+c+\dfrac{1}{abc}\)
4. Cho a,b,c là các số thực dương thỏa mãn \(a+b+c+ab+bc+ac=6\) . Tính Max của \(C=abc\)
5. Cho a,b,c là các số thực dương thỏa mãn \(a+b+c=2\) . Tính Max của \(D=abc\left(a+b\right)\left(b+c\right)\left(c+a\right)\)
Giúp mk nhanh nhé mn ơi
Câu 3. Dự đoán dấu "=" khi \(a=b=c=\frac{1}{\sqrt{3}}\)
Dùng phương pháp chọn điểm rơi thôi :)
LG
Áp dụng bđt Cô-si được \(a^2+b^2+c^2\ge3\sqrt[3]{a^2b^2c^2}\)
\(\Rightarrow1\ge3\sqrt[3]{a^2b^2c^2}\)
\(\Rightarrow\frac{1}{3}\ge\sqrt[3]{a^2b^2c^2}\)
\(\Rightarrow\frac{1}{27}\ge a^2b^2c^2\)
\(\Rightarrow\frac{1}{\sqrt{27}}\ge abc\)
Khi đó :\(B=a+b+c+\frac{1}{abc}\)
\(=a+b+c+\frac{1}{9abc}+\frac{8}{9abc}\)
\(\ge4\sqrt[4]{abc.\frac{1}{9abc}}+\frac{8}{9.\frac{1}{\sqrt{27}}}\)
\(=4\sqrt[4]{\frac{1}{9}}+\frac{8\sqrt{27}}{9}=\frac{4}{\sqrt[4]{9}}+\frac{8}{\sqrt{3}}=\frac{4}{\sqrt{3}}+\frac{8}{\sqrt{3}}=\frac{12}{\sqrt{3}}=4\sqrt{3}\)
Dấu "=" \(\Leftrightarrow a=b=c=\frac{1}{\sqrt{3}}\)
Vậy .........
2, \(A=\frac{a^2}{b+c}+\frac{b^2}{a+c}+\frac{c^2}{a+b}\)
\(A=\frac{a^2}{b+c}+\frac{b^2}{a+c}+\frac{c^2}{a+b}\)
\(A=\left[\frac{a^2}{b+c}+\frac{\left(b+c\right)}{4}\right]+\left[\frac{b^2}{a+c}+\frac{\left(a+c\right)}{4}\right]+\left[\frac{c^2}{a+b}+\frac{\left(a+b\right)}{4}\right]-\frac{\left(a+b+c\right)}{2}\)
Áp dụng BĐT AM-GM ta có:
\(A\ge2.\sqrt{\frac{a^2}{4}}+2.\sqrt{\frac{b^2}{4}}+2.\sqrt{\frac{c^2}{4}}-\frac{\left(a+b+c\right)}{2}\)
\(A\ge a+b+c-\frac{6}{2}\)
\(A\ge6-3\)
\(A\ge3\)
Dấu " = " xảy ra \(\Leftrightarrow\)\(\frac{a^2}{b+c}=\frac{b+c}{4}\Leftrightarrow4a^2=\left(b+c\right)^2\Leftrightarrow2a=b+c\)(1)
\(\frac{b^2}{a+c}=\frac{a+c}{4}\Leftrightarrow4b^2=\left(a+c\right)^2\Leftrightarrow2b=a+c\)(2)
\(\frac{c^2}{a+b}=\frac{a+b}{4}\Leftrightarrow4c^2=\left(a+b\right)^2\Leftrightarrow2c=a+b\)(3)
Lấy \(\left(1\right)-\left(3\right)\)ta có:
\(2a-2c=c+b-a-b=c-a\)
\(\Rightarrow2a-2c-c+a=0\)
\(\Leftrightarrow3.\left(a-c\right)=0\)
\(\Leftrightarrow a-c=0\Leftrightarrow a=c\)
Chứng minh tương tự ta có: \(\hept{\begin{cases}b=c\\a=b\end{cases}}\)
\(\Rightarrow a=b=c=2\)
Vậy \(A_{min}=3\Leftrightarrow a=b=c=2\)
Ta có: \(a+b+c+ab+bc+ca=6\)
Áp dụng BĐT AM-GM ta có:
\(a+b+c+ab+bc+ca\ge6.\sqrt[6]{\left(abc\right)^3}\)
\(\Leftrightarrow6\ge6.\sqrt[6]{\left(abc\right)^3}\)
\(\Leftrightarrow1\ge\sqrt[6]{\left(abc\right)^3}\)
\(\Leftrightarrow1\ge\left(abc\right)^3\)
\(\Leftrightarrow1\ge abc\)
\(\Leftrightarrow1\ge C\)
Dấu " = " xảy ra \(\Leftrightarrow a=b=c=ab=bc=ca\Leftrightarrow a=b=c=1\)
Vậy \(C_{max}=1\Leftrightarrow a=b=c=1\)
Cho a,b,c là các số thực dương thỏa mãn: abc=1. Chứng minh rằng:
\(\frac{1}{\sqrt{a^5-a^2+3ab+6}}+\frac{1}{\sqrt{b^5-b^2+3bc+6}}+\frac{1}{\sqrt{c^5-c^2+3ac+6}}\le1\)
Cho a,b,c,d là các số thực dương thỏa mãn a+b=c+d và a^2+b^2=c^2+d^2.Tính a^2021 + b^2021 = c^2021+d^2021